KLD(Kullback-Leibler Divergence)
쿨백-라이블러 발산(Kullback–Leibler divergence, KLD)은 두 확률분포의 차이를 계산하는 데에 사용하는 함수로, 어떤 이상적인 분포에 대해, 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다.
-Wikipedia-
KLD는 두 확률분포 사이의 다름을 측정한다. 주의해야 할 점은, KLD는 두 분포 사이의 거리가 아니라는 것이다.
KLD의 수식과, 예시를 보면서 같이 개념을 이해해보자.
두 확률분포 p와 q가 있다고 할 때, p 관점에서 측정한($x$를 sampling 할 때 p에서 sampling) KLD의 수식은 다음과 같다.
$$KL(p||q) = -\mathbb{E}_{x\sim p(x)}\left[\log \frac{q(x)}{p(x)} \right]$$
$$ = -\int p(x)\log \frac{q(x)}{p(x)}{d}x$$
다음과 같은 분포들이 있다고 해보자

확률분포 p에서 sampling 된 $x$가 있을 때, $q_1(x)$는 $q_2(x)$보다 큰 것을 확인할 수 있다.
따라서 다음과 같은 결과가 도출된다.


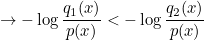
예시를 보면, 직관적으로 $q_1$이 $q_2$에 비해 $p$에 근접한 분포임을 확인할 수 있다.
따라서, KL-Divergence는 덜 비슷할수록 큰 값, 비슷할수록 작은 값을 지니며, 두 분포가 같을 경우 0의 값을 가짐을 알 수 있다.
이러한 KL-Divergence는 분포 간의 dissimilarity를 측정해주기 때문에, groud truth 확률분포와 DNN이 나타내는 확률분포의 dissimiliarity를 minimize 하는 과정에 사용할 수 있다.
Entropy, Cross-Entropy
정보(Information)란?
정보라는 것은, 간단하게 말하면 불확실성(Uncertainty)을 나타낸다.
$$I(X) = -\log P(X)$$
확률이 낮아질수록 불확실성은 높아지기 때문에 정보량은 올라가고, 확률이 높을수록 불확실성이 낮아지기 때문에 정보량도 낮아진다.
Entropy
Entropy란, 정보량의 기댓값을 의미한다. 즉, 불확실성의 평균인 셈이다.

Cross-Entropy
그렇다면, Cross-Entropy는 무엇일까? 두 분포 $p$와$q$가 있다고 할 때, 분포 $p$에서 바라본 $q$의 정보량의 평균을 의미한다.
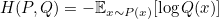
Cross-Entropy는 KL-Divergence와 마찬가지로 두 분포가 비슷할수록 작은 값을 가진다.
이 또한 예시와 함께 살펴보겠다.

아까와 같은 예시이다. 마찬가지로 확률분포 p에서 sampling 된 $x$가 있을 때 $q_1(x)$는 $q_2(x)$보다 큰 것을 확인할 수 있다.
즉, 다음과 같다


예시를 보면, 직관적으로 $q_1$이 $q_2$에 비해 $p$에 근접한 분포임을 확인할 수 있다. 즉, 분포가 $p$에 가까울수록 작은 값을 가지는 것이 확인되었다.
Cross-Entropy 또한 groud truth 확률분포와 DNN이 나타내는 확률분포의 dissimiliarity를 minimize 하는 과정에 사용할 수 있다.
보통 Classification 문제에서 Loss function을 Cross-Entropy를 사용하여 경사 하강법을 통한 Loss 최소화 작업을 하는 이유도 이 때문이다. (Cross-Entropy값이 작아질수록 두 분포가 비슷해지는 것이기 때문)
'ML&DL' 카테고리의 다른 글
| RNN(Recurrent Neural Network)이란? (2) | 2022.12.01 |
|---|---|
| [논문 리뷰] Mixed Precision Training (0) | 2022.11.29 |
| Likelihood(가능도)와 MLE(Maximum Likelihood Estimation)란? (3) | 2022.07.22 |
| 경사 하강법(Gradient Descent)이란?? (0) | 2022.07.18 |




댓글