언어 모델(Language Model)
언어 모델(Language Model)이란, 문장의 확률을 나타낸 모델이다. 즉
- 문장 자체의 출현 확률을 예측
- 이전 단어들이 주어졌을 때, 다음 단어를 예측
과 같은 기능을 위한 모델인 것이다.
예시와 함께 알아보겠다.
중고 맥북프로 14인치 모델 130만원에 OOO
다음과 같은 예시에서 빈칸에 아래와 같은 선택지를 고를 수 있다면, 어떤 것을 고를 것인가?
- 먹습니다
- 팝니다
- 모릅니다
- 맛있다
일반적으로, 2번 팝니다를 고를 것이다.
인간의 두뇌에는 문맥, 즉 단어와 단어 사이의 확률이 학습이 되어있기 때문에 2번 "팝니다"를 무리없이 고를 수 있다.
이러한 Task를 모방하기 위해, 많은 문장들을 수집하여 단어와 단어 사이의 출현 빈도를 세어 확률을 계산하는것이 언어 모델(Language Model)이라고 할 수 있다.
따라서, 언어 모델(Language Model)의 궁극적인 목표는, 우리가 일상 생활에서 사용하는 언어의 문장 분포를 정확하게 모델링(모사)하는 것이다.
언어 모델(Language Model)의 수식
그렇다면, 이러한 언어 모델을 수식과 함께 알아보자

수식을 하나씩 살펴보자
$x_{1:n} = \{x_1,...,x_n\}$은 문장 $x$는 n개의 단어로 구성된다는 의미이다.
$\sum_{i=1}^{N}\log P(x_{1:n}^i;\theta)$는 log-likelihood로, ground truth로부터 나온 sample(dataset)을 분포 $\theta$가 얼마나 설명하는지 나타낸다. 즉, sample들을 분포가 얼마나 잘 설명하는지를 나타낸다. 여기서의 sample은 문장으로, $N$개의 문장을 모아놓은 dataset에 포함된 문장이다.
따라서, 이러한 sample을 분포가 얼마나 잘 설명하는지 나타내는 log-likelihood를 최대화하기 위해 $ \text{arg}\max$를 사용한다.
likelihood와 log-likelihood에 관해서는 아래의 글에서 다뤘었다.
Likelihood(가능도)와 MLE(Maximum Likelihood Estimation)란?
통계학에서, 가능도(可能度, 영어: likelihood) 또는 우도(尤度)는 확률 분포의 모수가, 어떤 확률변수의 표집값과 일관되는 정도를 나타내는 값이다. 구체적으로, 주어진 표집값에 대한 모수의 가
gbdai.tistory.com
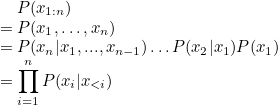
아까의 수식의 정의에 따라 $P(x_{1:n})$은 $P(x_1, \dots , x_n)$으로 바꿔쓸 수 있다.
이를 풀어쓰면 $P(x_n|x_1,...,x_{n-1})\ldots P(x_2|x_1) P(x_1)$이 되는데, 이는 곧 $\prod_{i=1}^{n}\log P(x_i|x_{<i})$이 된다.
이렇게 나온 수식에 $\log$를 취해주면

다음과 같은 형태가 나오게 된다. (양변에 $\log$를 취해주면서 곱이 summation으로 변환됨)
그렇다면, 이 형태를 아까 봤었던 수식에 적용해보자
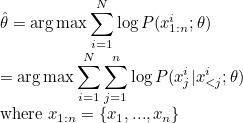
여기서, $i$는 각 문장을 의미하고, $j$는 각 단어를 의미한다.
즉, 위 수식은 각 $i$번째 문장에서, $j$이전까지의 단어가 주어졌을때, $j$번째 단어가 나올 확률을 최대화해주는 분포 $\theta$를 찾는 것이다.
언어 모델(Language Model)의 사용
이러한 언어 모델(Language Model)은 크게 두 가지 역할을 할 수 있다.
- 여러개의 문장이 주어졌을 때 가장 좋은 문장 고르기
$x^1$과 $x^2$의 두 문장이 있다고 가정해보자. $\theta$를 parameter로 가지는 언어모델이 있을 때, 두 문장을 언어 모델에 넣어서 문장 출현 확률을 구할 수 있다. $P(x^1;\theta) < P(x^2;\theta)$이라 하면, $x^2$문장의 출현 확률이 더 큰 것이기 때문에, 보다 좋은 문장이라고 할 수 있다.
- 주어진 단어들의 다음 단어를 예측하기
단어들이 주어졌을 때, 그것을 바탕으로 한 다음 단어의 확률 분포가 있을 것이다. 해당 분포를 maximize하는 단어를 찾아 다음 단어로 하게 함으로써 다음 단어를 예측한다. 이를 여러 번 반복하면 문장이 생성되고, 이는 자연어생성(NLG) task가 된다.
N-gram Language Model
다음의 문장을 살펴보자
<BOS> You are everything I see<EOS>
주어진 문장의 확률분포를 modeling하는 P(<BOS> You are everything I see <EOS>)를 구해보자.
이는 다음과 같이 나타낼 수 있다.

그리고, 아래의 확률 값은 다음과 같이 word sequence를 corpus에서 count함으로써 확률값을 approximate할 수 있다.
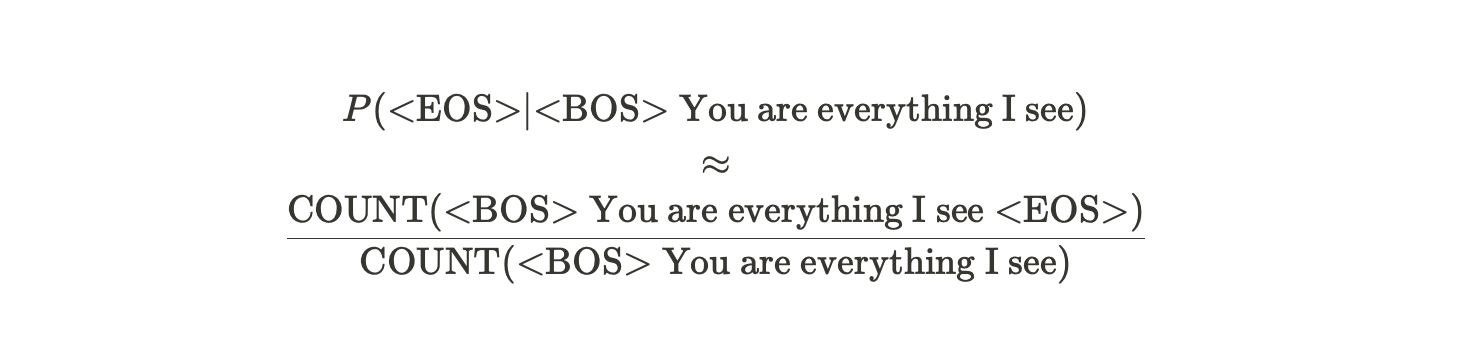
이러한 과정을 일반화해서 표현한다면, 다음과 같은 수식이 나온다.
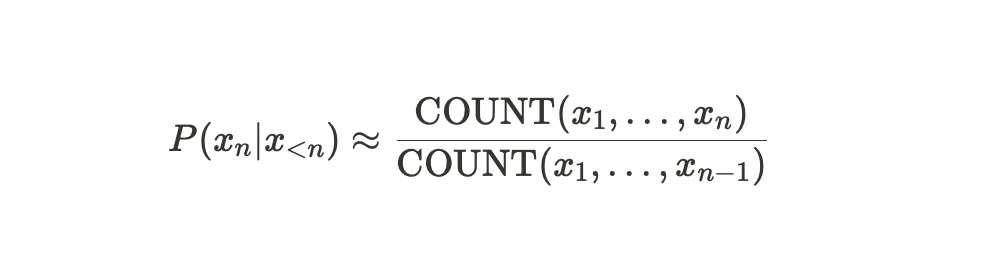
즉, $n-1$번째 단어까지 주어졌을 때, $n$번째 단어의 확률값은$x_1, \dots ,x_{n}$의 sequence를 세어보고 $x_1, \dots ,x_{n-1}$의 sequence를 corpus에서 세어본 값으로 나눈 값으로 approximate될 수 있다는 것이다.
그런데, 만약 해당 sequence가 없다면 어떻게 될까? $x_1, \dots ,x_{n}$의 sequence나 $x_1, \dots ,x_{n-1}$의 sequence 둘 중 하나라도 corpus에서 등장하지 않아 count값이 0이라면 확률값도 0이 되어버리는 문제가 발생하게 된다.
그렇다면, corpus에서 등장하지 않는 문장에 대해서는 확률값을 구할 수 없을까?
이러한 문제를 해결하기 위해 Markov Assumption을 적용한다.
Markov Assumption
Markov Assumption이란, 이전의 모든 단어를 보고 확률값을 approximate를 하는것이 아니라, k개의 단어만 보고 확률값을 approximate하는 것이다.
만약, k가 2일 경우, 2개의 단어만 보고 확률값을 approximate하는 것이며 수식은 다음과 같이 변경된다
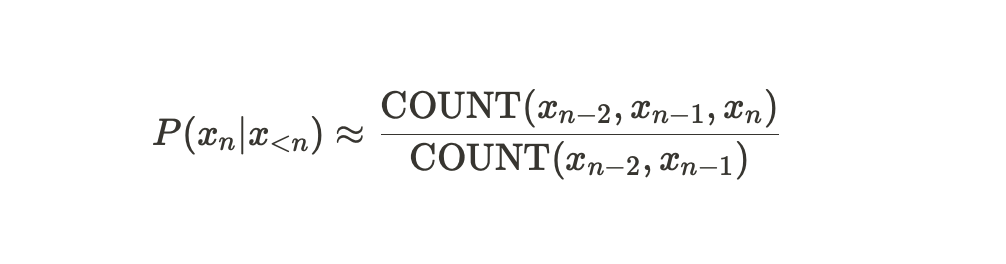
이렇게 하는 이유가 무엇일까? 아래의 예시 문장과 함께 살펴보자
Same bed but it feels just a little bit bigger now Our song on the radio but it don't sound the same
이 예시 문장과 처음부터 끝까지 일치하는 문장이 corpus에 존재할 가능성이 있을까? 결론적으로, 거의 없다.
이렇게 corpus에 문장이 없으면, 기존 방식으로는 count값이 0이 되어버려 확률이 0이 되어버린다.
이러한 문제를 해결하기 위해, 전체를 다 보지 않고 k개씩만 잘라서 보는 것이다. 위의 문장에서 k는 3이라고 가정하고, radio 위치에 있는 단어의 확률값을 approximate한다면, "song on the" 를 본다. 이러한 "song on the" 는 corpus에 있을 가능성이 전체 문장보다 높다.
즉, count값이 0이 되어버릴 가능성이 적어지는 것이다.
이처럼, Markov Assumption을 통해, corpus에서 등장하지 않는 문장에 대해서는 확률값을 구할 수 있다.
이러한 성질을 문장 단위로 확대하여 적용해보자
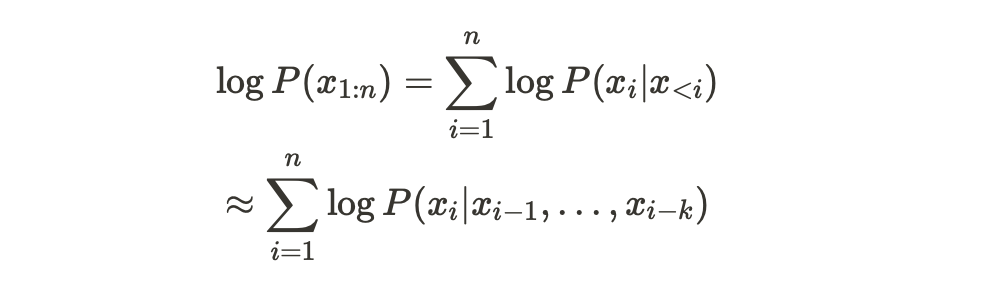
다음과 같은 형태로 적용됨을 확인할 수 있다.
N-gram
k가 1일 경우에는, 이전의 1개의 단어와 자기 자신을 보기 때문에 2개의 단어를 보게 된다.
k가 2일 경우에는, 이전의 2개의 단어와 자기 자신을 보기 때문에 3개의 단어를 보게 된다.
즉, N-gram에서 N은 k+1 이며, k에 따른 N-gram의 명칭 변화를 아래에 정리해보겠다.
| K | N-gram | Name |
| 0 | 1-gram | Uni-gram |
| 1 | 2-gram | Bi-gram |
| 2 | 3-gram | Tri-gram |
※ 4-gram부터는 four-gram의 형식으로 명명된다
이러한 N-gram은 n이 커지면 많이 보기 때문에 확률이 정확하게 표현될 것이라는 생각과는 달리,
n이 커질수록 확률이 정확하게 표현되기 어렵다.
'NLP' 카테고리의 다른 글
| [논문 리뷰] Neural Machine Translation by Jointly Learning to Align and Translate - Bahdanau Attention (0) | 2022.12.04 |
|---|---|
| Attention이란?-원리부터 masking까지 (General Luong Attention을 기반으로) (0) | 2022.11.25 |
| 시퀀스-투-시퀀스(Sequence-to-Sequence, seq2seq)란? - 기본 구조편 (0) | 2022.11.22 |
| 워드 임베딩(Word Embedding)이란? (1) (0) | 2022.09.04 |
| Tokenization(토큰화)란 무엇일까? (0) | 2022.08.20 |




댓글