이번 게시물에서는 Big Bird를 제시한 논문인 Big Bird: Transformers for Longer Sequences에 대해 다뤄보도록 하겠다.
해당 논문은 2020년도 NeurIPS에 소개되었다.
원문 링크는 다음과 같다.
Big Bird: Transformers for Longer Sequences
Transformers-based models, such as BERT, have been one of the most successful deep learning models for NLP. Unfortunately, one of their core limitations is the quadratic dependency (mainly in terms of memory) on the sequence length due to their full attent
arxiv.org
Introduction
논문이 작성될 당시, self-attention mechanism을 기반으로 한 Transformer를 골자로 하는 BERT와 같은 아키텍쳐들이 다양한 NLP task에서 활약하고 있었다. 이러한 Transformer 기반의 아키텍쳐들은 기존의 RNN계열(LSTM, GRU) 기반의 아키텍쳐들에서 발생했던 sequential dependency를 제거하고, input sequence 안의 개별 token이 sequence의 모든 다른 각각의 token에 대해 독립적으로 작용하게끔 함으로써 RNN계열 아키텍쳐들의 한계점을 해결하였다.
그러나, 이러한 self-attention mechanism은 sequence의 길이가 증가하면 계산량은 quadratic하게 늘어난다는 특징을 가지고 있고, 이러한 현상은 corpus의 길이가 길어도 context(model에 제공하는 sequence)의 길이를 제한시킨다는 한계를 지닌다.
이러한 한계점을 해결하여 long context를 요구하는 다양한 task에서의 성능 향상을 이루어내기 위해, 저자들은 본 논문에서 sparse attention mechanism을 사용하는 새로운 아키텍쳐인 BIGBIRD를 제안한다. 저자들이 제안하는 sparse attention mechanism은 계산 복잡도가 token의 개수에 따라 선형적으로 증가($O(n)$)한다는 특징을 가지고 있다. (full-quadratic self-attention은 $O(n^2 \cdot d)$)
이러한 BIGBIRD는 다음과 같은 세 가지의 주요한 요소로 구성되어진다.
- sequence의 모든 부분을 참고하는 $g$개의 global tokens
- 모든 token들은 local neighboring token인 $w$의 집합을 참고한다.
- 모든 token들은 $r$개의 random token들을 참고한다.
이 부분에 대한 자세한 설명은 뒷부분에 다루도록 하겠다.
이러한 방법론들을 적용한 BIGBIRD는 기존 self-attention mechanism을 적용한 아키텍쳐들보다 8배정도 긴 sequence length를 가진 task에서도 높은 성능을 유지했다고 한다.
BIGBIRD Architecture
우선, BIGBIRD는 기존 full-attention mechanism이 아닌, generalized attention mechanism을 사용한다.
이러한 Generalized attention mechanism에 대해 차근차근 알아가보자.
먼저 input sequence의 token 개수만큼의 vertex(node)를 가지는 directed graph(유향 그래프) $D$가 있다고 가정해보자.
Directed graph $D$에서의 edge들은 attention mechanism으로 인해 발생하는 inner product를 의미한다.
예시를 통해 알아보자. "There are too many papers to read!" 라는 예시가 있다고 가정해보자.

"There are too many papers to read!"를 통해 위와 같은 Input sequence $X$가 만들어짐을 확인할 수 있다.
해당 input sequence를 통해 생성되는 directed graph $D$는 다음과 같다.

token의 개수만큼 vertex가 생성되고, 해당 vertex들을 edge가 연결하는 것을 확인할 수 있다. 위에서 이야기했듯이, directed graph $D$에서의 edge들은 attention mechanism으로 인해 발생하는 inner product를 의미한다.

Graph의 edge에 따르면, 8번 token이 3번 token을 참고하고, 7번 token이 4번 token을 참고하기 때문에 8번과 7번이 각각 Query의 역할, 3번과 4번이 Value의 역할을 한다.
이에 따라 $x_8$과 $x_3$, $x_7$과 $x_4$는 각각 서로 inner product를 진행한다. (이는 dot-product attention mechanism과 동일하다)
이때, directed graph $D$의 임의의 vertex $i$의 out-neighbor들의 집합을 $N(i)$라고 정의한다.
(Out-neighbor란, directed graph(유향 그래프)에서 해당 vertex로부터 나가는 edge가 존재하는 다른 vertex들을 의미한다. 위의 예제에서는 vertex 8의 out-neighbor는 vertex 3이 되고, 그 역은 성립하지 않는다.)
최종적으로, generalized attention mechanism의 $i$번째 output vector는 다음과 같이 정의된다.
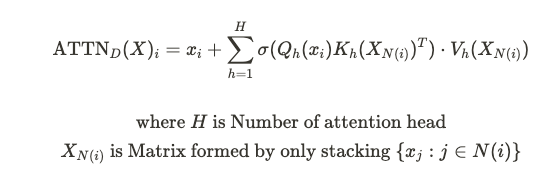
여기서, $X_{N(i)}$는 전체 input이 아닌, $N(i)$의 원소들로 구성된 모든 $j$를 통해 골라진 $x_j$를 의미한다.
즉, 기존 attention mechanism과는 다르게, 선택된 항목들끼리만 dot product 연산을 진행하는 것이다.
(만약 directed graph $D$가 complete graph, 즉 완전 그래프였다면 기존 attention mechanism과 같다.)
해당 설명은 인접 행렬을 통해 더욱 간단해질 수 있다. Directed graph $D$에 대한 adjacency matrix(인접 행렬) $A$가 있다고 가정해보자.
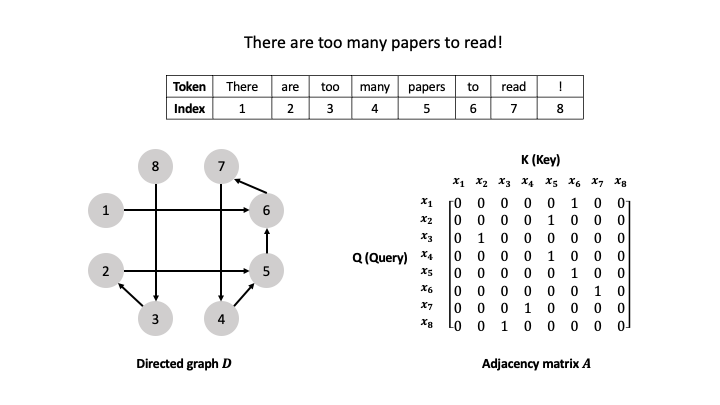
인접 행렬에서 row($i$)는 Q(Query)의 역할을, column($j$)는 K(Key)의 역할을 한다.
예시 중에서, graph $D$를 보면 3번 vertex에서 2번 vertex로의 edge가 존재하는데, 이는 곧 $x_3$이 $x_2$의 정보를 참고(내적 연산이 일어남)한다는 뜻이며, 이를 인접 행렬에서는 $A(3,2) = 1$로 표현한다. 아무런 연결이 없는 경우에는 해당 위치를 0으로 표현한다. 위 예시는 해당 규칙에 따라 좌측의 그래프를 우측의 인접 행렬로 나타낸 예시이다.
즉, BERT와 같이 fully-quadratic attention mechanism을 사용하는 아키텍쳐들은 adjacency matrix $A$의 모든 행과 열이 1로 표현되는 것이다.
이렇게 self-attention을 그래프와 인접 행렬로 표현함으로써, self-attention의 quadratic complexity를 줄이는 과정 또한 graph sparsification 문제로 접근할 수 있게 된다. Graph sparsification이란, 그래프의 구조적인 특성은 유지하면서 edge의 수를 줄이는 것을 목표로 하는 task이다. 기존의 연구에 따르면, random graph를 확장시켜 complete graph (완전 그래프)를 근사할 수 있다고 한다. 이는 곧 기존 fully-quadratic attention mechanism을 근사하는 것과 같은 맥락이다. 저자들은 이러한 성질을 본 새로운 아키텍쳐에 적용시키기 전에, attention mechanism을 위한 sparse random graph는 다음과 같은 두 가지의 성질을 가져야 한다고 말한다.
- small average path length between vertex
- notion of locality
이 성질들에 대해 추가적으로 살펴보자
Small average path length between vertex
논문에서는 가장 간단한 random graph model인 Erd˝os-Rényi model을 예시로 든다. Erd˝os-Rényi model이란, vertex 사이에 edge가 생길 확률이 일정한 graph generative model이다.
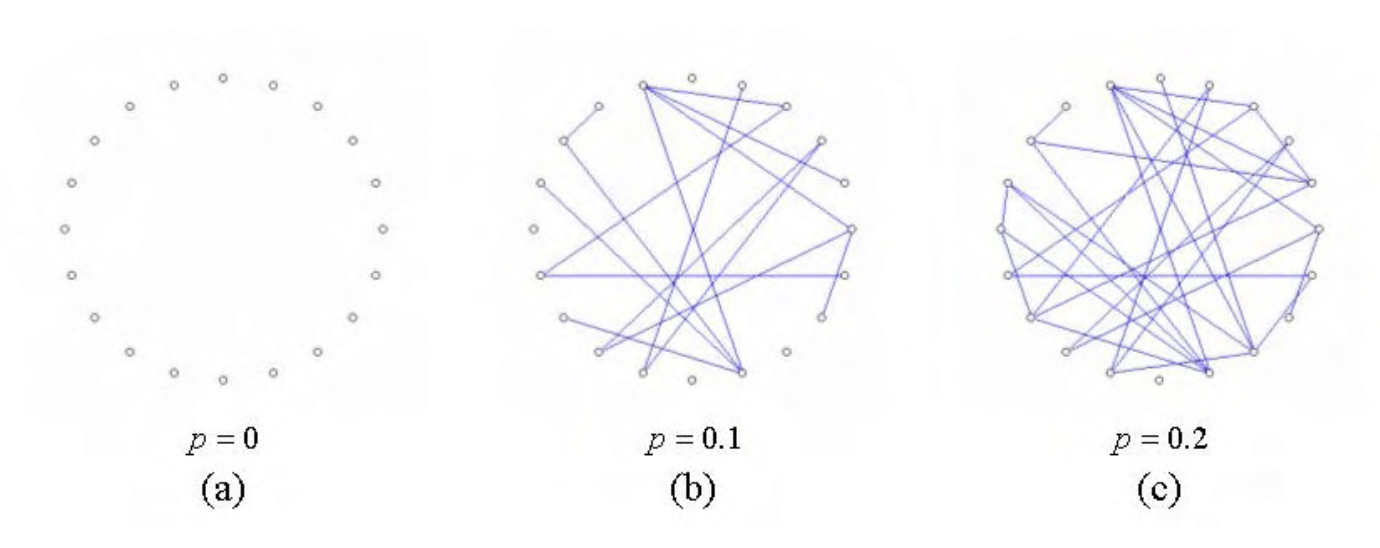
선행된 연구들에서, 이러한 random graph에서의 edge의 개수가 선형적으로 증가할수록 임의의 두 vertex 사이의 shortest path의 개수는 로그 함수를 따른다는 것이 증명되었다. 즉, random graph의 크기를 키운 뒤 sparse한 graph로 만들어도 임의의 두 vertex 사이의 shortest path의 개수의 변화량은 매우 작다는 것이다. 결과적으로 이러한 random graph는 complete graph를 근사할 수 있게 된다.
이러한 사실에 입각하여, 저자들은 Query가 $r$개의 random한 key를 참고하는 sparse attention을 제안한다.
Notion of Locality
위의 random sparse attention에 이어서, 저자들은 BIGBIRD를 구성하는 또 다른 구성 요소를 소개한다.
저자들은 대부분의 NLP task와 computational biology의 context가 상당수의 locality of reference를 보이는 것에 주목한다.
Locality of reference이란, token에 관련된 상당수의 정보가 해당 token의 인접 token으로부터 기인하는 현상을 말한다. 실제로 논문에서 언급된 선행 연구들 중, NLP task에서의 self attention을 연구한 결과에 따르면, 대상 token의 representation과 인접해있는 token의 representation의 inner product가 매우 중요했다고 한다.
저자들은 이러한 현상을 그래프 이론으로 설명하려 한다. 그래프 이론에서, clustering coefficient는 임의의 vertex가 존재할 때, 해당 vertex에 이웃하는 vertex들이 얼마나 잘 연결되어 있는지를 측정하는 metric이며, 1인 경우에는 모든 이웃 vertex가 서로 연결되어 있는 것이고, 0이면 모든 이웃 vertex들이 서로 연결되어있지 않은 것이다.
이는 다음과 같은 수식을 통해 계산 가능하다.

즉, clustering coefficient가 높으면 clique, 혹은 near-clique가 많은 것이라고 볼 수 있다.
(clique : 그래프 이론에서 clique란, complete graph(완전 그래프)인 부분 그래프를 의미한다.)
정리하자면, clustering coefficient가 높다는 것은 다음과 같이 정의할 수 있다.
=> clustering coefficient가 높다
= clique가 높다
= Attention을 나타내는 그래프 $D$에서, complete graph인 부분 그래프의 개수가 많다
= 임의의 token에 관련된 정보 중 상당수가 인접 token으로부터 기인한다.
저자들은 Erd˝os-Rényi model의 경우 clustering coefficient가 높지 않지만, small world graph와 같은 random graph의 종류들은 clustering coefficient가 높다는 결과를 도출한 선행 연구를 제시하면서, context 안의 local structure를 포착하기 위한 방법론으로 Window attention을 제시한다.
이는, window의 크기 $w$가 주어질 때, $i$번째 위치의 token은 양옆으로 $w/2$개의 token을 참고하는 attention이다.
(Word2vec을 떠올리면 이해가 쉬워진다.) 이를 인접 행렬로 나타내게 되면 다음과 같다.
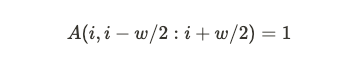
Window 안에 위치한 token들에 대해서만 정보를 참고하고, 그 외의 token에 대해서는 참고하지 않는다.
이를 시각화하면 다음과 같다.

논문에서는 지금까지 소개된 random attention과 window attention으로 실험을 진행하였는데, 이 두 가지 요소만으로는 BERT의 성능을 따라잡는 context를 만들 수 없었다고 한다.
따라서, 저자들은 실험과 이론적인 분석을 통해 "global token"의 중요성을 인지하고, 이를 추가하기로 하였다.
Global token
여기서, Global token이란, 원래의 self-attention mechanism처럼 모든 token에 대해 dot product를 통한 attention 계산을 하는 token을 말한다.
즉, 해당 global token들은 인접 행렬 $A$에서 항상 1의 값을 가지는 것이다.
BIGBIRD에서 이러한 global token은 다음과 같은 두 종류가 있다.
- BIGBIRD-ITC : 이미 존재하는 token을 "global token"으로 만듬
- BIGBIRD-ETC : CLS와 같이 추가적인 "global token"을 추가
BIGBIRD에서는 $g$개의 global token을 추가한다. 이를 인접 행렬로 나타내면, 다음과 같다.

수식을 차근차근 살펴보자.
먼저 인접행렬 $A$에, 추가되는 global token의 개수 $g$만큼의 row와 column을 더해준 인접 행렬 $B$를 생성한다.
이렇게 생성된 인접행렬 $B$에 대해, 1부터 $N$까지의 모든 $i$와 $j$중에 $B(g+i, g+i)$는 $A(i, j)$와 같다는 수식이다.
이렇게 추가적인 global token을 더하는 것을 통해 context를 더 많이 저장할 수 있게 되었고, 이를 통해 성능이 향상된 것을 실험으로 확인할 수 있었다고 한다.
BIGBIRD
최종적으로, BIGBIRD 아키텍쳐에서 사용되는 attention mechanism은 위에서 언급된, 아래의 3가지의 방법론을 더한다.
- Query가 $r$개의 random Key를 참고하는 attention
- 각각의 Query가 현재 위치 기준으로 양옆으로 $w/2$개의 token을 참고하는 attention
- $g$개의 global token
정리하자면, Q(Query)가 K(Key)의 모든 token을 참고하는 것이 아닌, 위 3가지의 방법론을 통해 참고할 Key를 선택하는 것이다.
이를 시각화하면 다음과 같다.

Experiments
본 논문에서는 NLP task와 genomics task에 BIGBIRD를 적용시키고, 다른 아키텍쳐들과 결과를 비교하였다.
QA task
HotpotQA, NaturalQ, TriviaQA, WikiHop으로 성능 평가 진행하였고 결과는 다음과 같다.
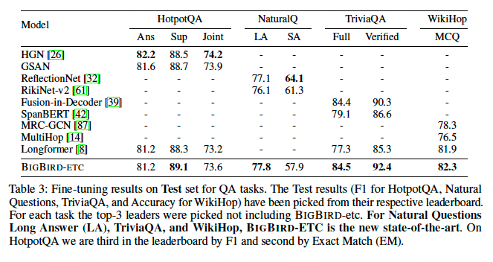
BIGBIRD는 QA task에서 전반적으로 좋은 성능을 보여주는 것을 확인할 수 있다.
Classification task
IMDb, Yelp-5, Arxiv, Patents, Hyperpartisan으로 성능 평가 진행하였다.
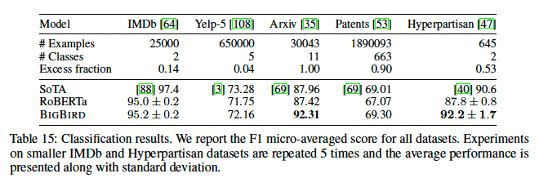
기존 아키텍쳐 대비 좋은 성능을 보였으며, 특히 Arxiv dataset과 같이 corpus의 길이가 더 길면서 학습 데이터의 개수가 적은 경우에 큰 성능 향상을 보였다.
Summarization task
Summarization task의 경우 Encoder-Decoder 구조로 진행하였으며, 이때 Encoder에만 sparse한 attention을 적용하였다. (대부분의 task 상황에서, output sequence의 길이가 input sequence의 길이보다 작기 때문이라고 한다.)
Arxiv, PubMed, BigPatent로 성능 평가 진행하였고 결과는 다음과 같다.
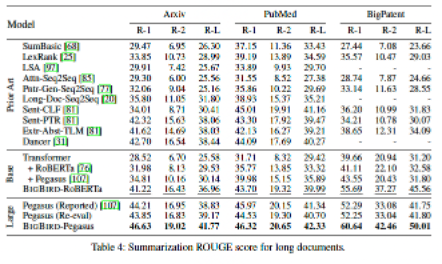
모든 dataset에서 SOTA를 달성하였으며, 길이가 긴 document뿐만 아니라 짧은 document에서도 좋은 성능을 보였다.
Genomics
논문에서는 길이가 긴 특징을 가진 DNA data에 대해서도 MLM pretraining 진행, 이후 관련 downstream task 진행하였다.
먼저, DNA에서 RNA를 합성하는 단계의 시작에 관여하는 유전자 영역 예측하는 task인 Promoter Region Prediction task의 결과이다.

타 아키텍쳐에 비해, BIGBIRD가 월등히 좋은 성능을 보여준다.
다음으로는, Non-coding DNA가 미치는 영향을 살펴보기 위한 Chromatin-Profile Prediction task를 진행하였다.
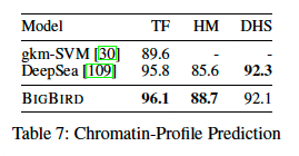
마찬가지로, BIGBIRD는 좋은 성능을 보여주었다. 결론적으로, 길이가 매우 긴 DNA data에 대해서도 BIGBIRD는 매우 좋은 성능을 보이는 것을 확인할 수 있었다.
이렇게 BIGBIRD에 대해 간략히 리뷰해보았다. Appendix에 포함된 수학적 증명, Turing Completeness관련 내용, GPU/TPU에서의 구현 등의 내용은 추후 다른 게시물에서 다뤄볼 예정이다.




댓글