정렬(Sort)이란?
정렬이란, 주어진 데이터를 정해진 기준에 따라 순서를 재배열하는 작업을 말한다.
정렬 알고리즘의 종류
매우 다양한 정렬 알고리즘이 존재하지만, 대표적인 것들만 나열해보면
- 버블 정렬(Bubble sort)
- 선택 정렬(Selection sort)
- 삽입 정렬(Insertion sort)
- 병합 정렬(Merge sort)
- 퀵 정렬(Quick sort)
등이 있다. 특히, 병합 정렬과 퀵 정렬은 복잡하지만 효율적인 정렬로 분류된다. 그렇다면, 모든 경우에 대해 퀵 정렬이나 병합 정렬을 적용하는것이 유리할까?
결론부터 말하자면, 그렇지 않다.
모든 경우에 대해 최적의 성능을 보여주는 정렬 알고리즘은 존재하지 않는다.
그렇기 때문에, 각 상황에 맞게 최적의 정렬 알고리즘을 선택하여 적용해야만 한다.
정렬 알고리즘의 평가
그렇다면, 정렬 알고리즘이 좋네 마네 하는 기준은 무엇일까? 바로 비교횟수와 이동횟수이다. 원소의 비교와 이동이 적을수록 좋은 정렬 알고리즘이고 많을 수록 좋지 못한 알고리즘이다.
이는 쉽게 생각해보면 당연한 것이다. 목표를 달성하기 위해 보다 적은 시간과 비용을 투자하는 방법은 효율적인 방법이다. 정렬 알고리즘도 이와 마찬가지이다.
정렬 알고리즘의 안정성
정렬 알고리즘은 안정성의 측면에서도 다음과 같이 나눌 수 있다.
- 안정된 정렬
- 안정되지 않은 정렬
두 항목의 차이는, 같은 값을 갖는 원소의 순서가 정렬 후에도 유지되느냐의 차이이다. 같은 값을 갖는 원소의 순서가 정렬 후에도 유지된다면, 안정된 정렬이고, 그렇지 못하면 안정되지 않은 정렬인 것이다. 그림과 함께 살펴보도록 하겠다.

다음과 같은 배열이 있다고 가정하겠다. 오름차순으로 정렬한다고 가정할 시, 순서는 10, 20, 30, 30, 40이 될 것이다. 그런데, 30의 값을 가지는 원소가 B와 D, 두개가 존재한다. 안정된 정렬과 안정되지 않은 정렬은 여기서 나뉘게 된다.
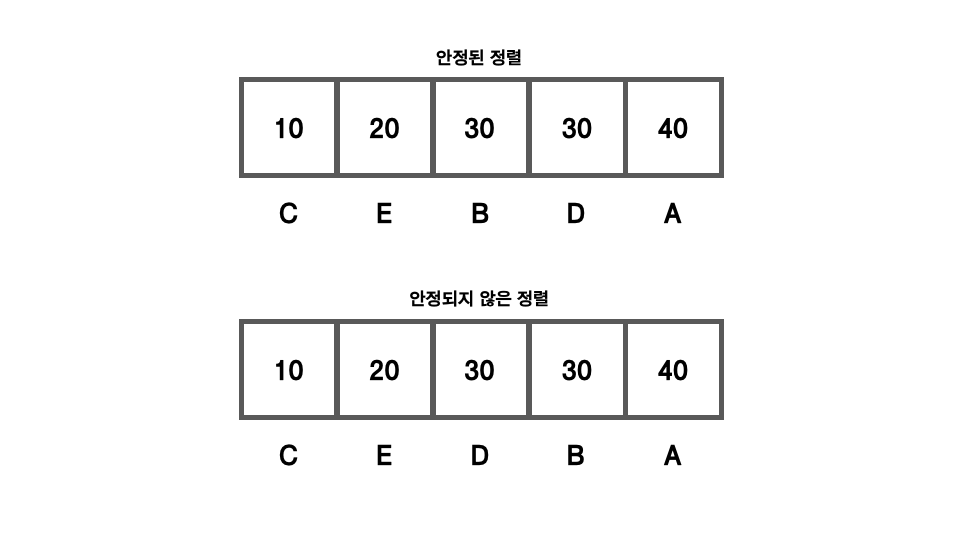
안정된 정렬과 안정되지 않은 정렬을 비교하면, 중복되는 값인 30의 정렬 결과가 달라짐을 볼 수 있다.
안정된 정렬의 경우, 원래 배열의 순서였던 B, D 순서대로 정렬됨을 확인할 수 있지만, 안정되지 않은 정렬에서는 원래 배열의 순서가 유지되지 않았음을 확인할 수 있다.
즉, 중복된 값을 가진 요소들이 존재할 경우, 해당 요소들에 한해 원래 배열의 순서가 유지되면 안정된 정렬, 그렇지 않으면 안정되지 않은 정렬인 것이다.
이제부터는 위에서 언급했던 배열 알고리즘의 종류에 대해 하나씩 살펴보겠다.
버블 정렬(Bubble sort)
버블 정렬이란, 정렬되지 않은 부분에서 인접한 두 원소의 크기를 비교하여 위치를 바꾸는 작업을 반복하는 정렬이다.
다음과 같이 정렬되지 않은 부분에서 하나하나 비교해가면서, 크기를 비교하고 자리를 바꿔가는 정렬이 버블 정렬이다.
이러한 버블 정렬은 O(n^2)의 시간 복잡도를 가진다.
버블 정렬의 구현
void bubble_sort(int data[], int n)
{
// 데이터의 개수만큼 반복
for (int i = 0; i < n - 1; ++i)
{
// 맨 뒤에서부터 정렬이 완료된 부분 뒤까지 반복
for (int j = n - 1; j > i; --j)
{
//만약 뒤 데이터보다 앞 데이터가 크다면, 위치를 바꿔준다
if (data[j] < data[j - 1])
swap(data[j], data[j - 1]);
}
}
}
선택 정렬 (Selection sort)
선택 정렬이란, 정렬되지 않은 원소들 중에서 최솟값 원소를 찾아 맨 왼쪽 원소와 교환하는 방식이다.
기본적으로 버블 정렬과 큰 틀에서는 같지만, 정렬되지 않은 범위에서 앞뒤 요소끼리 크기를 비교했던 버블 정렬과 다르게 최솟값으로 지정된 요소와 크기 비교를 하고, 더 작은 원소가 등장하면 최솟값을 갱신한다. 이후 해당 최솟값의 위치와 맨 왼쪽 원소와 교환한다.
정리해보면
- 맨 오른쪽부터 시작하여, 첫 원소를 최솟값으로 설정한다.
- 정렬되지 않은 부분을 순회하며, 최솟값을 갱신한다.
- 갱신된 최솟값과 맨 왼쪽 요소와 위치를 교환한다.
- 3번까지의 과정 반복
의 과정이다. 선택 정렬 또한 O(n^2)의 시간 복잡도를 가진다.
선택 정렬의 구현
void selection_sort(int data[], int n)
{
for (int i = 0; i < n - 1; ++i)
{
//최솟값의 위치 저장
int minimum = i;
for (int j = i + 1; j < n; ++j)
{
// 두 번째 반복문에서는 정렬되지 않은 부분을 순회하며
// 최솟값과 크기 비교
if (data[j] < data[minimum])
minimum = j;
}
swap(data[i], data[minimum]);
}
}
'CS' 카테고리의 다른 글
| [자료구조] 해시 테이블(Hash Table)이란? (0) | 2022.08.21 |
|---|---|
| [자료구조] 트리(Tree)와 이진 트리(Binary tree)란? (0) | 2022.07.24 |
| [자료구조] 큐(Queue)의 개념과 구현(2) (0) | 2022.07.11 |
| [자료구조] 큐(Queue)의 개념과 구현(1) (0) | 2022.07.11 |
| [자료구조] 연결 리스트(Linked list)와 구현 (2) (0) | 2022.06.27 |




댓글