[논문 리뷰] Attention is all you need - transformer란?

이번 글에서는 Attention is all you need 논문을 살펴봄과 동시에 논문에서 제시하는 아키텍처이자, 현재로서는 매우 중요해진 transformer에 대해 살펴보도록 하겠다. 논문 링크는 아래와 같다.

Attention Is All You Need

 

Transformer

해당 논문이 발표되었던 시기에는 NLP와 같은 sequential task를 수행하기 위해 RNN계열의 아키텍처들(LSTM, GRU)을 사용해왔다.

그러나, 이러한 RNN계열의 아키텍처들은 이전 timestep의 hidden state가 현재 timestep의 input으로 들어오는 순차성 때문에 병렬화가 어려워 학습 시간이 길다는 단점과 sequence의 길이가 길어졌을 때 메모리 제약으로 인한 capacity의 하락으로 인해 성능이 하락한다는 단점이 있다.

 

이러한 RNN계열의 아키텍처의 문제를 해결하기 위해 다양한 연구들이 진행되었고, 그중에서 attention이라는 개념이 도입되었다. attention에 대해서는

Attention이란?-원리부터 masking까지

이 게시물에 정리해놨다.

추가적으로, Bahdanau attention과 Luong attention이 제시된 눈문들도

[논문 리뷰] Effective Approaches to Attention-based Neural Machine Translation - Luong Attention

[논문 리뷰] Neural Machine Translation by Jointly Learning to Align and Translate - Bahdanau Attention

위의 게시물들에 정리해놨다.

Attention을 통해 sequence길이가 길어졌을 때 성능 하락을 어느 정도 해결할 수 있었지만, 몇 가지 경우를 제외하면 attention은 RNN계열의 아키텍처들하고만 사용되어 왔다.

 

그래서 논문에서는, seq2 seq과 같은 기존의 방법론에서 RNN계열의 아키텍처, 즉 recurrence를 제거해버리고, attention으로만 구성한 아키텍처인 transformer를 제시하였다. 이는 병렬화를 가능케하고, 보다 짧은 시간을 학습했음에도 SOTA의 성능을 낼 수 있다고 한다.

 

 

Background

이 당시에 sequential computation을 줄이기 위해,  ByteNet, ConvS2S와 같이 CNN을 사용하여 모든 input, output position에 대해 병렬적으로 hidden representation을 계산하는 연구 결과들이 발표되었었다.

그러나, 이러한 ByteNet, ConvS2S와 같은 model들은 임의의 두 input position과 output position를 relate 시키기 위해 필요한 작업량이 두 postion의 거리가 멀어질수록 증가하는 문제점이 있다(ConvS2S는 선형적으로 증가하고, ByteNet은 logarithmically 하게 증가)

 

논문에서 제안하는 Transformer는 해당 relate를 위해 필요한 작업량이 오로지 상수 번의 작업만을 필요로 한다.

이 과정에서 타 model 대비 부족해지는 effective resolution의 경우에는 Multi-Head-Attention으로 대응한다고 한다.

 

 

Model Architecture

모델의 전반적인 구성은 아래와 같다.

Figure 1: The Transformer - model architecture.

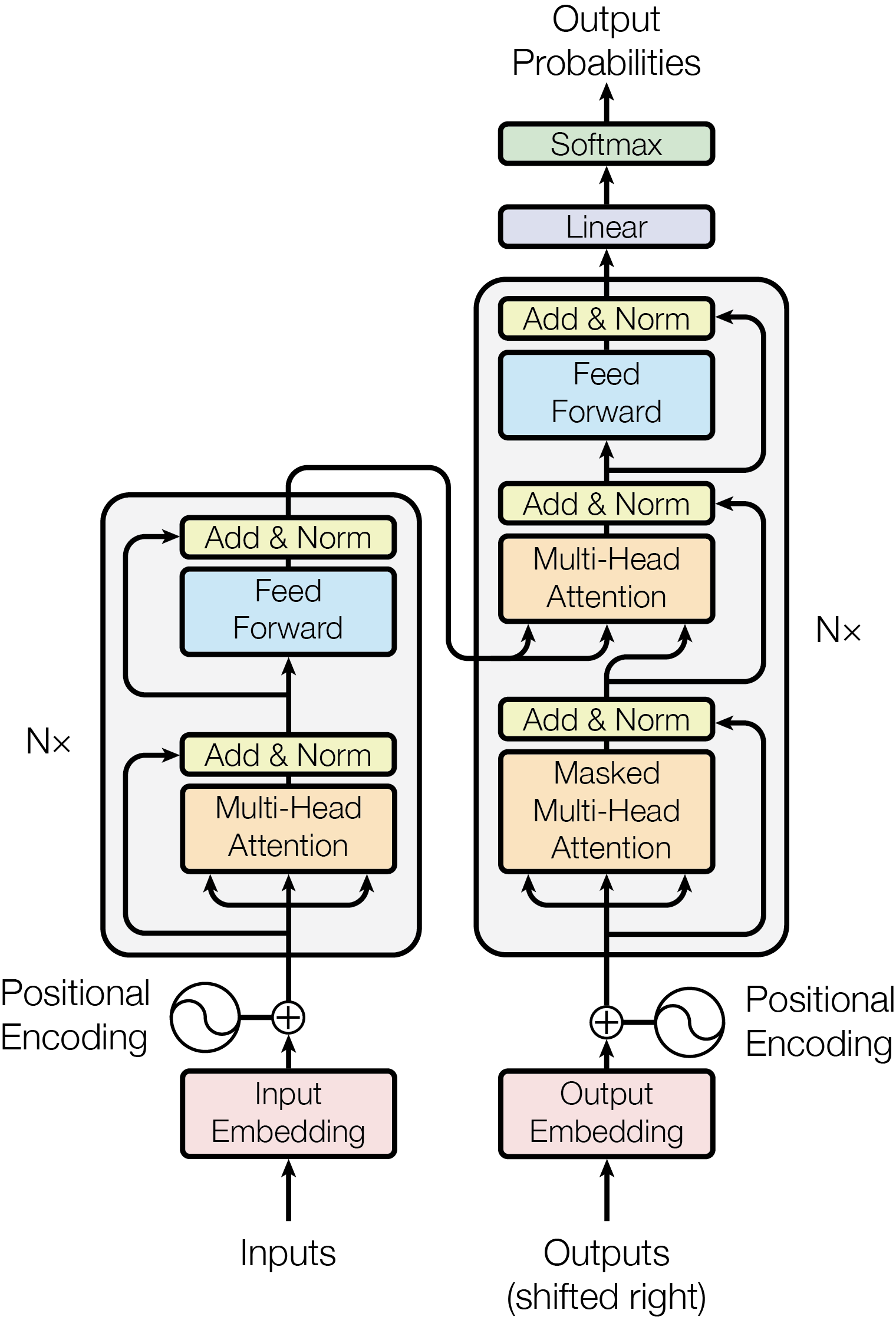
논문에서 제시한 순서대로 모델 구성을 하나씩 살펴보도록 하겠다.

 

우선, transformer는 seq2 seq와 비슷하게 크게 Encoder 부분과 Decoder 부분으로 나눌 수 있다. 

각각의 Encoder와 Decoder의 역할과 구조를 나눠서 살펴보겠다.

 

Encoder

Encoder의 경우, 6개의 layer로 구성되어있으며 (여기서 말하는 layer는 위 그림에서 보이는 encoder block 1개를 의미한다),

해당 layer의 경우 multi-head self attention과 feed-forward network의, 2개의 sub-layer로 구성되어있다.

또한, 각 sub-layer마다 residual connection과 layer normalization를 사용하였다. 논문에서는 이러한 residual connection을 용이하게 하기 위해 embedding layer뿐만 아니라 모든 sub-layer가 512차원의 output을 생성하게끔 설계했다고 한다.

정리하자면, Encoder 안에는 다음과 같은 요소들이 포함되어 있다.

 

• Multi-head self attention
• Position-wise Feed-Forward Networks
• Residual connection
• Layer normalization

 

Decoder

Decoder 또한 , 6개의 layer로 구성되어있으며(마찬가지로,  layer는 위 그림에서 보이는 decoder block 1개를 의미한다),

encoder에서 사용되었던 multi-head self attention과 feed-forward network의 2개의 sub-layer와 더불어 encoder로부터 넘어오는 output에 대한 multi-head attention을 수행하는 추가적인 sub-layer로 구성되어있다. encoder와 마찬가지로 sub-layer마다 residual connection과 layer normalization를 사용하였다.

그런데, encoder로부터 넘어오는 output에 대한 multi-head attention이 아닌, output embedding으로부터 input을 받는 sub-layer의 경우에는 multi-head self attention이 아니라 masked multi-head self attention이라고 표시되어있다. 이는 왜 그럴까?

 

decoder의 경우, encoder와 다르게 autoregressive 한 속성을 가지고 있다

즉, timestep $t$의 output을 만들 때, timestep $t-1, t-2 \dots $만을 참고하여 output을 만들어 내야 한다. 

이러한 특성 때문에, 현재 timestep보다 미래의 timestep은 참고하지 않도록, attention weight를 계산할 때 masking을 활용하여,  softmax가 적용되기 전 음의 무한대 값을 넣고, attention weight가 계산된 후에는 0의 값을 가지게 하여 미래의 timestep에 대한 정보를 차단하게 된다.

따라서 output embedding으로부터 input을 받는 sub-layer의 경우에는 multi-head self attention이 아니라 masked multi-head self attention이 되는 것이다.

 

Decoder에 대해서 정리해보면, Decoder 안에는 다음과 같은 요소들이 포함되어 있다.

 

• Multi-head self attention - encoder로부터 넘어오는 output에 대한 multi-head attention
• Masked multi-head attention
• Position-wise Feed-Forward Networks
• Residual connection
• Layer normalization

 

 

Scaled Dot-Product Attention

 

Figure 2: (left) Scaled Dot-Product Attention

Scaled Dot-Product Attention의 수식은 다음과 같다

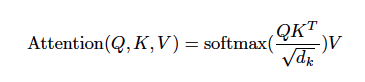
우선, Scaled Dot-Product Attention을 설명하기 전에, Dot-Product Attention에 대해 잠깐 설명하고 넘어가도록 하겠다.

Dot-Product Attention은 위에서도 잠깐 언급된 논문인 Effective Approaches to Attention-based Neural Machine Translation이라는 논문에서 다음과 같이 소개되었다.

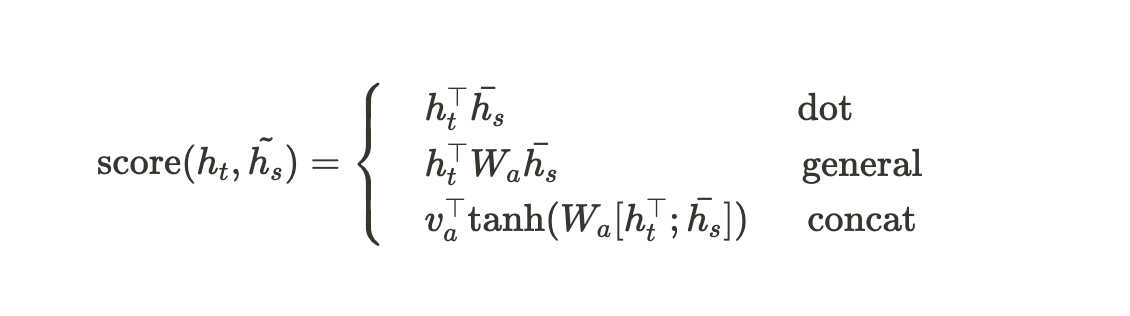
여기서 맨 위의 dot 부분이 Dot-product Attention이다.

해당 논문에서 $h_t^{\top}$는 현재 timestep의 Decoder의 hidden state matrix의 transpose를 나타내고, $\bar {h_s}$는 모든 timestep에서 Encoder의 모든 hidden state matrix를 나타낸다.

Dot-Product Attention이 소개된 논문에서는 LSTM을 사용했기 때문에 hidden state이며, 우리가 지금 살펴보는 Attention is all you need 논문에서는 $h_t^{\top}$가 Q(Query), $\bar {h_s}$가 K(Key)의 역할을 한다.

다시 돌아와서, Q(Query)와 K(Key)의 행렬곱을 하면 안에서는 각 timestep마다 Dot-Product 연산(내적 연산)이 일어나게 되는데, 이 Dot-Product 연산(내적 연산)을 통해 두 벡터의 유사도를 구하고, 이를 softmax를 취해 weigth vector를 구한 다음, V(Value)에 곱하여 context vector를 산출하는 과정이다.

Dot-Product Attention은 최적화된 행렬곱 연산으로 구현될 수 있기 때문에, 매우 빠르고 메모리 사용 측면에 있어서도 효과적인 장점이 있다.

그러나, Q(Query)혹은 K(Key)의 dimension인 $d_k$가 클 경우, Dot-product Attention의 성능이 하락하는 문제가 발생한다.

논문에서는 해당 성능 하락 원인을  $d_k$가 클 경우 Dot-product 값이 비약적으로 커지게 되면서, softmax의 기울기가 평평한 곳으로 값이 유도되기 때문이라고 추측한다.

 

Scaled Dot-Product Attention은 이러한 문제를 해결하기 위해 제안된다.

Dot-product Attention에 $\sqrt{d_k}$, Q(Query) 혹은 K(Key)의 dimension인 $d_k$의 제곱근으로 나눠 scaling을 해줌으로써, softmax의 입력값으로 Dot-product 값을 입력했을 때 기울기가 평평한 곳으로 유도되지 않게끔 대응하는 방법이다.

 

 

Multi-Head Attention

Figure 2: (right) Multi-Head Attention

서론에서 잠깐 이야기했던 Multi-Head-Attention이다. 타 model 대비 부족해지는 effective resolution을 대응하기 위해 고안되었으며, 작동 원리는 다음과 같다.

 

1. Q(Query)와 K(Key), V(Value)를 각각 linear transform 시킨다
2. linear transformed 된 Q(Query), K(Key), V(Value)에 대해 Scaled Dot-Product Attention을 수행한다.
3. 1번과 2번 과정을 h번 병렬적으로 수행한다
4. 병렬적으로 수행된 h개의 Scaled Dot-Product Attention의 결과(Head라고 표현한다)를 concat 한다.
5. concat 된 값을 다시 한번 linear transform 수행한다.

이에 대한 수식은 다음과 같다.

논문에서는 Head의 개수 $h$는 8개로 설정하였으며,  $d_k=d_v=d_{\text{model}}/h=64$로 설정하였다.

(앞서 Encoder와 Decoder를 다룰 때 $d_{\text{model}}$은 512라고 언급했었다.)

어찌 보면 원래 512차원이었던 Q(Query)와 K(Key), V(Value)가  linear transform 과정을 거치면서 64차원으로 줄어들고, 추후 concat 과정에서 다시 512차원으로 복구되는 것인데, 논문에서는 이러한 dimension reducing 과정을 통해 head가 h 개여도, computational cost는 full dimensionality의 single head attention과 동일하다고 말한다.

 

이러한 Multi-Head-Attentiondms reprehension 공간을 넓혀주는 장점이 있다.

 

Applications of Attention in Transformer

이제, 지금까지 알아본 Multi-Head-Attention이 Transformer에서 어떻게 응용되어 사용되는지 알아보자.

논문에서는 Transformer에서 Multi-Head-Attention을 아래의 3가지 방법으로 다르게 사용한다고 한다.

 

• encoder-decoder attention
  • Decoder Block에 위치해있으며, Q(Query)는 이전 Decoder layer에서 받으며, K(Key)와 V(Value)는 Encoder의 output에서 받는 Multi-Head-Attention이다.
• encoder contains self attention layers
  • Encoder Block에 위치한 Multi-Head-Attention이다.
• self-attention layer in decoder
  • Decoder Block에 위치해있으며, encoder-decoder attention과 다르게 output embedding으로부터 Q(Query), K(Key), V(Value) 모두를 받는다.
  • model figure에서 Masked Multi-Head-Attention이라고 명시되어있는 곳이다.
  • Decoder의 auto-regressive 한 속성 때문에, 미래의 timestep에 attention이 들어가는 것을 방지하기 위해 미래 timestep에 masking을 하였고, 이러한 특성 때문에 Masked Multi-Head-Attention이라고 한다. (masking에 관해서는 위에 링크된 게시물 참고 바란다)

 

Position-wise Feed-Forward Networks

Position-wise Feed-Forward Networks는 간단하게 다음과 같이 이루어져 있다.

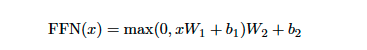
두 번의 linear transform과 한 번의 ReLU activation function으로 이루어져 있다.

position마다 개별적으로 동일한 parameter가 적용되지만, layer마다의 parameter는 다르다는 것을 유의해야 한다.

 

Position-wise Feed-Forward Networks의 input과 output size는 $d_{\text{model}}$, 즉 512이며, 은닉층 size는 2048이다.

 

 

Embeddings and softmax

Transformer 모델에 sequence를 input으로 넣기 위해, sequence token vector를 $d_{\text{model}}$, 즉 512의 dimension을 가진 vector로 변환해주는 Embedding layer를 사용한다는 것을 모델 구조에 대해 전반적으로 설명할 때 언급했었다.

또한, decoder의 output을 바탕으로 softmax를 취해 next-token probability를 구하는 과정에서도, $d_{\text{model}}$의 dimension을 가진 decoder의 output vector를 sequence token vector의 dimension으로 linear transform 해주는,

Pre-softmax linear transformation layer가 존재한다.

 

논문에서는, Encoder와 Decoder 부분에 각각 존재하는  Embedding layer와, Decoder에만 존재하는 Pre-softmax linear transformation layer의 weight를 공유한다고 한다. 

추가적으로, Embedding layers에는 공유되는 shared weight에 $\sqrt{d_k}$를 곱해준다고 한다.

 

논문에서 이 기법을 다루면서 언급한 논문이 있는데, 아래의 링크는 해당 논문에 대한 리뷰이다

[논문 리뷰] Using the Output Embedding to Improve Language Models - Weight tying

 

 

Positional Encoding

Transformer는 reccurence와 convolution을 사용하지 않기 때문에, sequence data를 다루기 위해서는 sequence 안의 token들에 위치 정보를 주입해야만 한다.

이 위치 정보를 주입해주는 것이 바로 Positional Encoding이다. input embedding에 Positional Encoding을 더해줌으로써 sequence 안의 token들에 위치 정보를 주입해주는 것이다.

Positional Encoding은 input embedding과 같은 $d_{\text{model}}$의 dimension을 가지고 있기 때문에 input embedding에 더할 수 있다.

논문에서 사용하는 Positional Encoding은 다음과 같다. (Sinusoidal Positional Encoding)

여기서 $pos$는 sequence에서 해당 단어의 위치인 position, $i$는 Positional Encoding의 dimension으로, 해당 Positional Encoding vector의 dimension이 짝수일 경우 위의 sin 공식을 이용하고, 홀수일 경우에는 cos 공식을 이용한다.

말로만 하면 이해가 힘들 수 있으니, 그림과 함께 살펴보도록 하자.

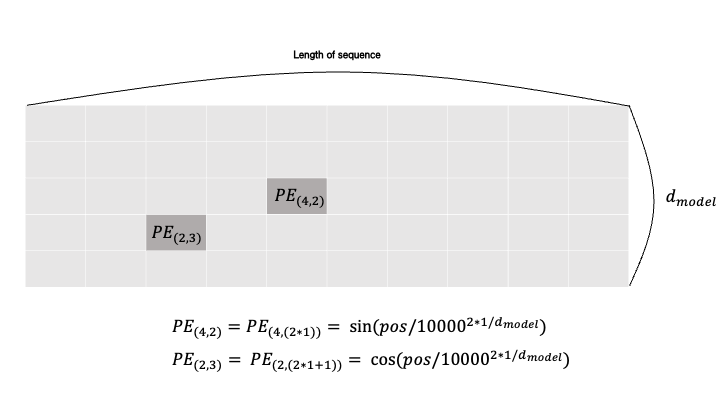
위 그림은 input embedding vector와 동일한 shape을 가진, Positional Encoding vector이다. 

$PE_{2,3}$부분을 먼저 보자. $PE_{2,3}$이란,  sequence에서 해당 단어의 위치인 position, $pos$는 2이며, Positional Encoding vector의 dimension인 $i$는 3이기 때문에, 가로 3번째, 세로 4번째의 칸에 위치해있다.(0부터 시작한다)

이때, i는 홀수이기 때문에 cos을 이용하는 식으로 Positional Encoding을 계산하여야 한다. 이렇게 계산된 $\cos(pos/10000^{2\times 1/d_{\text{model}}})$ 값은 Positional Encoding vector의 $PE_{2,3}$ 위치에 들어가게 된다.

 

$PE_{4,2}$도 마찬가지이다. sequence에서 해당 단어의 위치인 position, $pos$는 4이며, Positional Encoding vector의 dimension인 $i$는 2이기 때문에, 가로 5번째, 세로 3번째의 칸에 위치해있다.(마찬가지로 0부터 시작한다)

이때, i는 짝수이기 때문에 sin을 이용하는 식으로 Positional Encoding을 계산하여야 하며, 이렇게 계산된 $\sin(pos/10000^{2\times 1/d_{\text{model}}})$ 값은 Positional Encoding vector의 $PE_{4,2}$ 위치에 들어가게 된다.

 

이와 같은 방식으로 Positional Encoding vector의 모든 $pos$와 $i$의 값을 계산하고, 이 vector를 input embedding vector에 더해줌으로써 위치 정보를 주입해줄 수 있다.

 

저자들은 Facebook이 ConvS2S를 발표할 때 제안한 Learned positional embedding으로도 실험해봤지만 성능적으로 위의

sinusoidal Positional Encoding과 성능적으로 차이가 없음을 확인했다. 

 

오히려, sinusoidal Positional Encoding이 학습 중 모델이 마주하는 sequence(train corpus)의 길이보다 더 긴 sequence 길이로 추론 가능한 점을 들어 sinusoidal Positional Encoding을 채택했다고 밝힌다.

 

Why Self-Attention

논문에서는 self attention과 RNN과 CNN을 세 가지 측면에서 비교한다.

비교 기준은 다음과 같다.

 

• Total computational complexity per layer
• Amount of computation that can be parallelized (minimum number of sequential operations required)
• Path length between long-range dependencies in the network
  • Long-range dependencies를 모델이 학습하게끔 하기 위해 정말 많은 시도들이 진행되어왔고(LSTM, GRU의 등장) 이를 위한 핵심 요소 중 하나는 forward and backward path의 length를 줄이는 것이다. (gradient vanishing 문제로 인해)
  • 이 path의 길이가 길어질수록 모델이 Long-range dependencies를 더 쉽게 학습할 수 있게 된다.

 

비교 결과는 다음과 같다.

결과를 보면, RNN계열 아키텍처가 $O(n)$의 sequential operation을 필요로 하지만, self-attention layer는 상수 번($O(1)$)의 sequential operation만 필요로 하는 것을 확인할 수 있다. 이는 self-attention layer가 더 많이 병렬화 작업을 수행할 수 있고, 이를 통해 학습 시간을 현저히 줄일 수 있다는 것이다.

 

계산 복잡도 측면(computational complexity)에서 바라봤을 때, self-attention layer는 $n$(sequence length)이 $d$(representation dimensionality) 보다 작을 때 RNN 계열의 아키텍처보다 더 적은 계산 복잡도를 가지는 것을 알 수 있다.

 

Maximum path length 측면에서도 self-attention이 가장 작은 Maximum path length을 가지는 것을 확인할 수 있다. 이를 통해 self-attention 기반 모델은 Long-range dependencies를 더 쉽게 학습할 수 있다.

 

 추가적으로, self-attention은 아래의 그림과 같이 interpretable(설명 가능한) 모델이라는 장점도 가지고 있다.

 

Training

standard WMT 2014 English-German dataset과 larger WMT 2014 English-French dataset으로 학습하였으며,

NVIDIA P100 GPU 8개로 학습을 진행했다고 한다.

 

Optimizer

$\beta_1=0.9, \beta_2=0.98, \epsilon=10^{-9}$의 Adam optimizer를 사용하였으며, 아래의 식을 이용하여 learning rate를 조정했다.

즉, warmup_step에 따라 linear 하게 learning rate을 증가시키다가, step_num에 따라 square root 한 값을 통해 점진적으로 learning rate를 줄여나갔다. (논문에서는 warmup_steps = 4000으로 설정했다고 한다)

 

Regularization

각각의 sub-layer의 output이 sub-layer의 input에 더해지고 normalized 되기 전에 dropout을 적용하는 Residual-Dropout을 적용하였고, Encoder와 Decoder 각각 Embedding vector와 positional encoding의 합에도 dropout을 적용했다.

(이때, Dropout rate$P_{drop}$는 0.1로 지정했다.)

 

 

Result

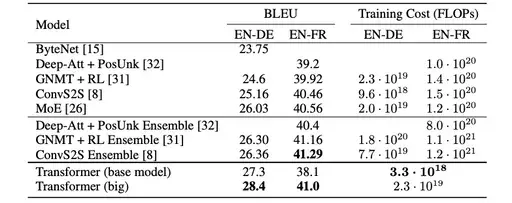
영어-> 독일어 번역 task에서 기존 model들보다 좋은 성능이 나옴을 확인할 수 있다. 심지어, 영어-> 프랑스어 번역 task에서는, 타 모델들을 ensemble 한 성능과 비슷함을 확인할 수 있다.

 

주목해야 할 점은 Training cost이다. 타 모델의 ensemble과 성능이 비슷하거나 높은 반면에, training cost는 압도적으로 적다.

이를 통해, Transformer는 성능은 높아졌지만, Training cost는 줄여줄 수 있는 모델임을 확인할 수 있다.

 

다음은 Tranformer model의 hyperparameter를 조정해가면서 실험한 결과이다

위 실험 결과를 통해 다음과 같은 정보를 알 수 있다.

 

• (A)를 확인해보면, single-head attention($h$=1)이 multi-head attention을 수행할 때보다 성능이 낮다.
• (B)에서는 Q(Query) 혹은 K(Key)의 dimension인 $d_k$를 낮추는 것이 성능 하락에 영향을 준다는 것을 알 수 있다.
• (C), (D)에서는 큰 모델일수록 성능이 좋고, dropout이 모델의 성능에 긍정적인 영향을 준다는 것을 알 수 있다.
• (E)에서는 논문에서 제시한 Positional embedding 기법이 아닌, Facebook이 ConvS2S를 발표할 때 제안한 Learned positional embedding을 써도 성능상의 차이가 없다는 것을 알 수 있다.

 

---

 

정말 중요한 논문이어서, 최대한 차근차근 꼼꼼히 살펴보았고, related work 중에서도 비중이 큰 연구면 논문을 읽어가며 진행한 터라, 시간이 오래 걸렸던 것 같다.

그렇지만 아직 못다 한 조사들도 있는 것 같아, 해당 논문에서 인용된 논문들도 꾸준히 리뷰하면서, 내용이 추가될 때마다 업데이트할 예정이다.