Echelon form(행사다리꼴)
Echelon form(행사다리꼴)이란, 다음의 특성을 가지는 행렬을 말한다.
- All nonzero rows are above any row of all zeros -> 0으로만 이루어진 행들은 맨 밑에 위치해야 한다
- Each leading entry(특정 행에서 제일 왼쪽에 있는 nonzero entry)of a row is in a column to the right of the leading entry of the row above it -> 특정 행의 leading entry가 자기 자신보다 위에 있는 leading entry보다 오른쪽에 있어야 함
예제와 함께 살펴보자

위의 행렬을 살펴보면,
- 모든nonzero row(0이 아닌 요소가 포함된 행)가 zeros(0으로만 이루어진 행) 위에 위치해 있고
- leading entry(특정 행에서 제일 왼쪽에 있는 nonzero entry) 1, 4, 6이 자기 자신보다 위에 있는 leading entry보다 오른쪽에 위치해있다.
따라서, 다음의 행렬은 위의 모든 조건을 만족하는 Echelon form, 행사다리꼴이다.
Row echelon form(기약 행사다리꼴)
Row echelon form(기약 행사다리꼴)은, Echelon form(행사다리꼴)의 특징에서 2가지를 추가적으로 만족시키는 행렬을 말한다.
Row echelon form(기약 행사다리꼴)이 되기 위한 조건을 정리해보자면,
- All nonzero rows are above any row of all zeros -> 0으로만 이루어진 행들은 맨 밑에 위치해야 한다
- Each leading entry(특정 행에서 제일 왼쪽에 있는 nonzero entry)of a row is in a column to the right of the leading entry of the row above it -> 특정 행의 leading entry가 자기 자신보다 위에 있는 leading entry보다 오른쪽에 있어야 함
- The leading entry in each nonzero row is 1 -> leading entry가 1이다
- Each leading 1 is the only nonzero entry in its column -> leading entry가 있는 열에서 leading entry를 제외하고 모두 0이어야만 한다.
3, 4번이 Echelon form(행사다리꼴)과 Row echelon form(기약 행사다리꼴)의 차이점이다.
마찬가지로, 예제와 같이 알아보도록 하겠다.

위의 행렬은 다음의 성질을 만족한다.
- 모든nonzero row(0이 아닌 요소가 포함된 행)가 zeros(0으로만 이루어진 행) 위에 위치해 있고
- leading entry(특정 행에서 제일 왼쪽에 있는 nonzero entry) 1, 4, 6이 자기 자신보다 위에 있는 leading entry보다 오른쪽에 위치해있다.
- 모든 leading entry가 1이다
- leading entry가 있는 1, 2,3번째 열에서, leading entry를 제외한 모든 요소는 0이다
따라서, 위의 행렬은 모든 조건을 만족하는 Row echelon form(기약 행사다리꼴)이다.
Row echelon form(기약 행사다리꼴)에서, leading entry 1의 위치를 pivot position이라고 한다.
이러한 Row echelon form(기약 행사다리꼴)에 대한 정의가 있는데 바로,
Each matrix is row equivalent to one and only one reduced echelon matrix
(각각의 행렬은 기약 행사다리꼴을 오로지 하나만 가진다)
이다. 즉 하나의 행렬이 두 개 이상의 기약 행사다리꼴을 가질 수 없다는 것이다.
Row reduction algorithm
Row reduction algorithm은 Row echelon form(기약 행사다리꼴)과 Echelon form(행사다리꼴)을 얻을 수 있는 방법이다.
이 방법은 Gauss-Jordan elimination(가우스-요르단 소거법)이라고도 불린다.
아래의 예시와 함께 하나씩 차근차근 따라가보자.

먼저, 가장 왼쪽에 위치한 nonzero column을 찾는다. 이때, 해당 column은 pivot column이라고 한다.

주황색 박스가 가장 왼쪽에 위치한 nonzero column이자, pivot column이다.
이 pivot column에서 pivot position은 column의 맨 위가 되는데, 위 예제에서는 pivot이 0이다.
이러한 경우에는 pivot column에서 nonzero entry를 찾은 뒤, 해당 nonzero entry가 속해있는 row와 pivot position위치의 row를 서로 바꿔준다.
예제에서는 2번째 row와 3번째 row 모두 교환 가능하며, 3번째 row와 교환하면서 과정을 진행해보겠다.

3이 pivot이 된 것을 확인할 수 있다.
이후, pivot position 밑을 Elementary row operation(기본 행 연산)의 replacement 연산을 활용하여 모두 0으로 만들어준다.
예제에서는 첫 번째 row에 -1을 곱한 것을 2번째 row에 더해주면 된다.
그러면 다음과 같은 결과가 나오게 된다
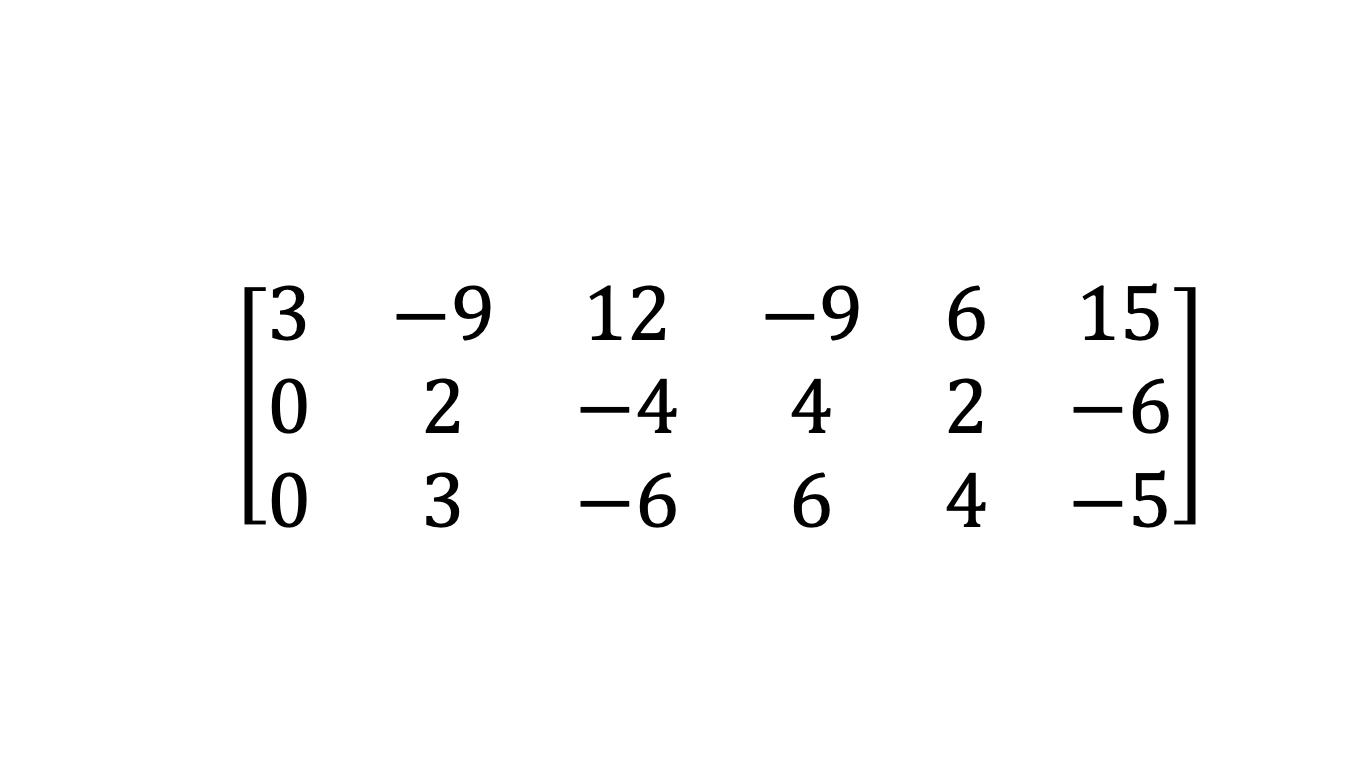
이후, 이 과정을 남아있는 submatrix에 대해 반복한다. submatrix란, 아래에서 주황 박스 안의 matrix를 의미한다.
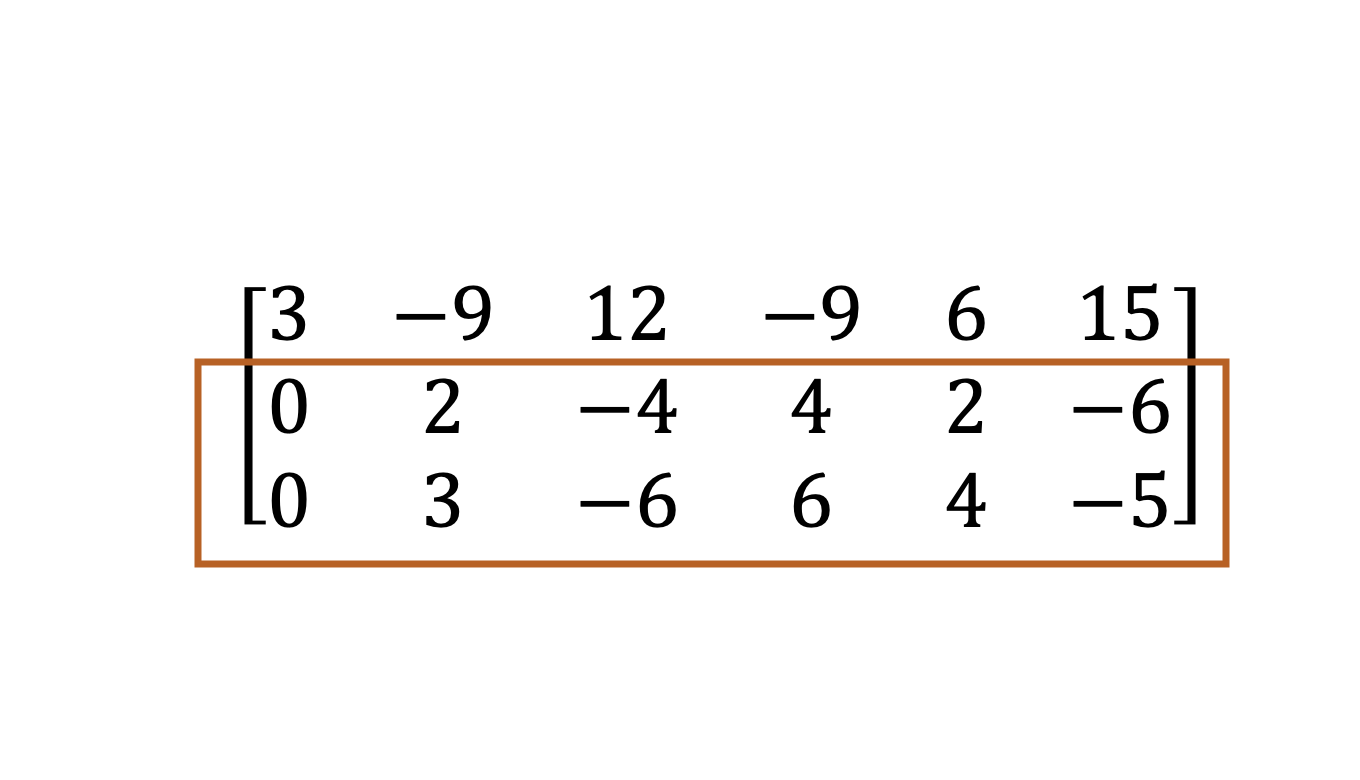
해당 submatrix에서 특정 행에서 제일 왼쪽에 있는 nonzero entry인 leading entry는 2이기 때문에 2를 pivot으로 설정하고, 해당 entry가 속해있는 두 번째 column을 새로운 pivot column으로 설정한다. 만약, 현재 2가 있는 pivot의 위치가 0이었으면 앞서 진행했던 것처럼 exchange 연산을 해줘야한다. 또한, submatrix의 해당 column이 모두 0이면 해당 부분은 건너뛴 이후 나머지 submatrix에 대해 위 과정을 수행한다.
예제로 돌아와서, pivot 밑을 0으로 만들어 주기 위해 2번째 row에 -3/2를 곱해준 값을 3번째 row에 더해주면, 다음과 같은 결과가 나오게 된다.

그러면 Echelon form(행사다리꼴)이 만들어지게 된다. 지금까지의 과정을 정리해보자면 다음과 같다.
- Begin with the leftmost nonzero column -> 가장 왼쪽의 nonzero column에서 시작한다.
- Select a nonzero entry in the pivot column as a pivot. If necessary, interchange rows to move this entry into the pivot position -> pivot column에서 pivot으로 nonzero entry를 선택하고, 필요시 interchange 연산 수행한다
- Row replacement to create zeros in all positions below the pivot -> replacement 연산을 이용하여 pivot 아래의 항목들을 모두 0으로 만든다
- Apply steps 1-3 to the submatrix that remain -> 1~3과정을 submatrix에 적용
이 과정은 forward phase라고 부르기도 하며, 이 forward phase를 통해 Echelon form(행사다리꼴)을 구할 수 있다.
이렇게 forward phase를 통해 구해진 echelon form(행사다리꼴)에서, 추가적인 과정을 통해 row echelon form(기약 행사다리꼴)을 만들 수 있다.
해당 과정은 다음과 같다.
- Beginning with the rightmost pivot and working upward and to the left, create zeros above each pivot. If a pivot is not 1, make it 1 by a scaling operation -> 맨 오른쪽 pivot부터 시작하여 pivot 위에 있는 요소들을 0으로 만들고, 왼쪽으로 이동한다. 만약 pivot이 1이 아니라면, scaling을 통해 1로 만들어준다.
아까 만들어 놓은 예제와 함께 살펴보자

우선 맨 오른쪽에 있는 pivot으로부터 시작해보자. 현재 상태에서 맨 오른쪽 pivot은 1인데, 해당 pivot이 1이기 때문에 scaling 과정은 생략한다. 그러면 pivot 위의 요소들을 0으로 만들 차례이다. 첫 번째 row에는 세 번째 row의 -6을 곱해서 더해주고, 두 번째 row에는 세 번째 row에 -2를 곱해서 더해보자.
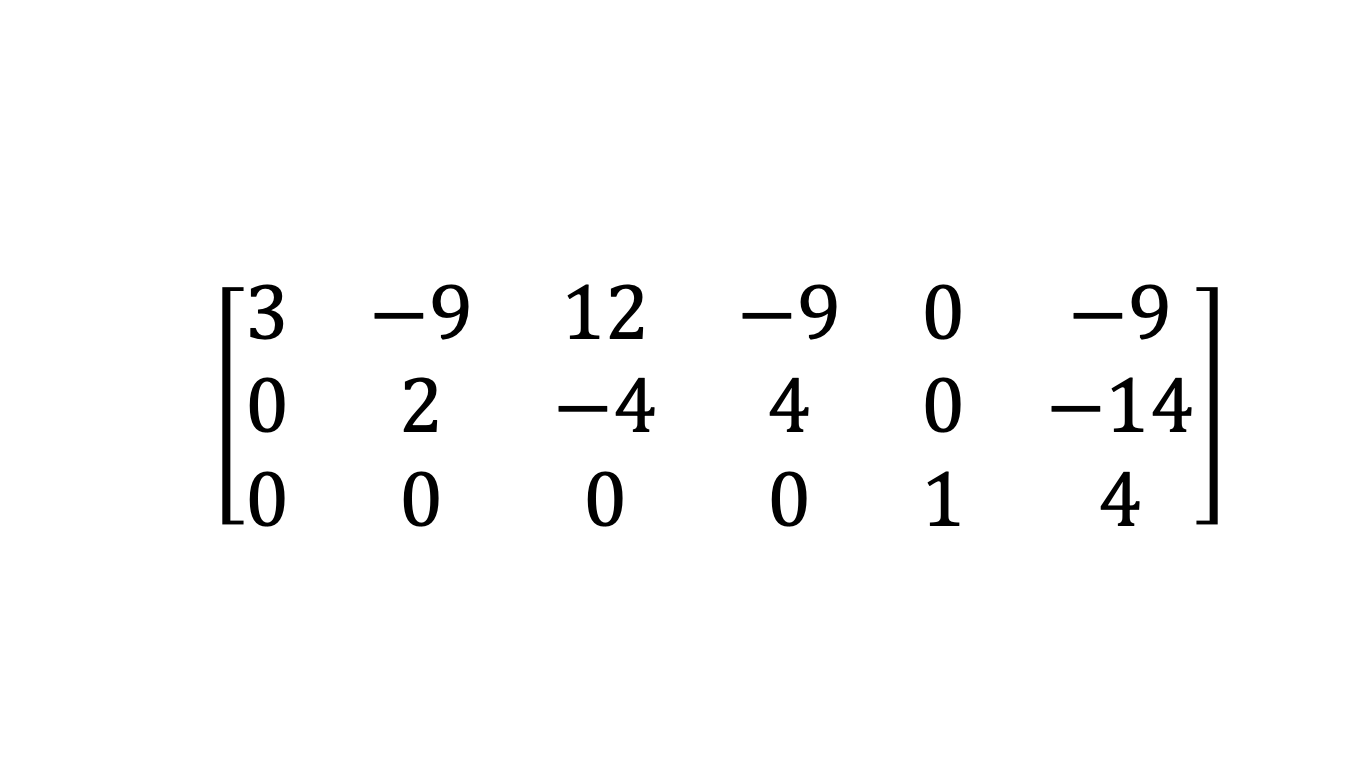
pivot 위의 요소들이 0이 되었으니, 다음 pivot으로 넘어가보자. 이번에는 두 번째 column에 있는 2가 pivot이다.
pivot이 1이 아니기에, 두 번째 row에 1/2를 곱해주어 1로 만들어보자.

이제 다시 pivot 위의 요소들을 0으로 만들어보자 두 번째 row에 9를 곱해서 첫 번째 row에 더해주자
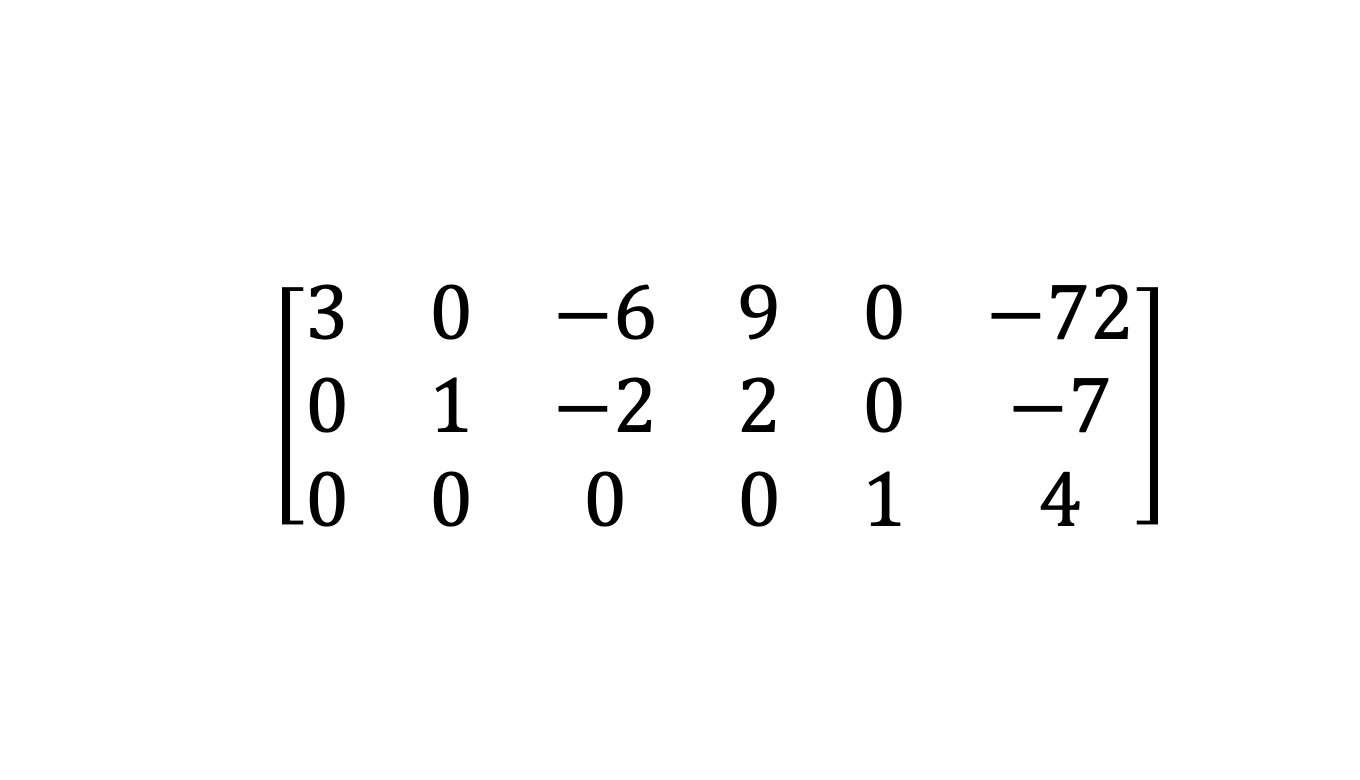
pivot 위의 요소들이 0이 되었으니, 다음 pivot으로 넘어가보자. 마지막으로, pivot이 3이기 때문에 1/3을 첫 번째 row에 곱해주어 scaling을 해주자
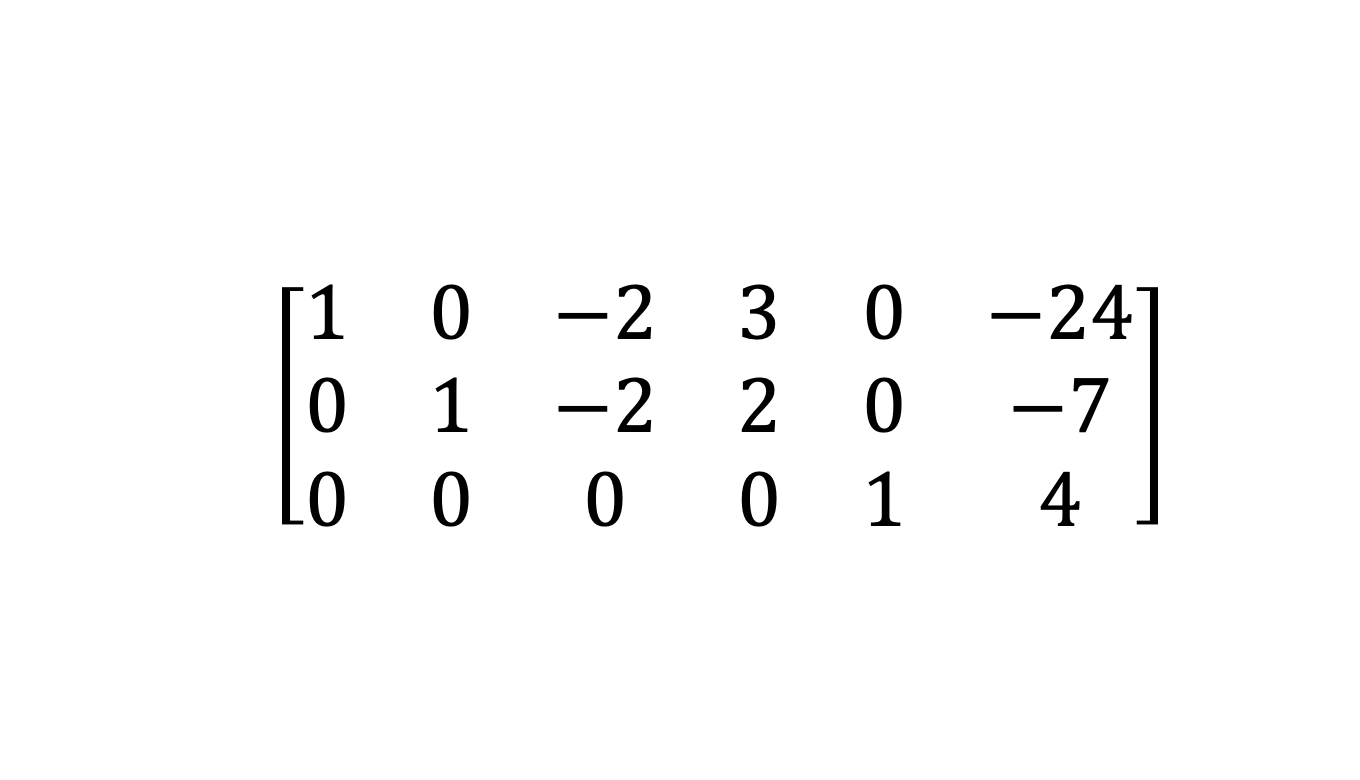
Row echelon form(기약 행사다리꼴)이 완성되었다.
금방까지의 과정은 backward phase라고 하며, 이 과정을 통해 Row echelon form(기약 행사다리꼴)를 구할 수 있다.
우리는 이렇게 구한 Row echelon form(기약 행사다리꼴)을 통해 linear system의 solution을 알 수 있다.
Solution of linear system
linear system에 관해서는 아래의 게시물에 정리되어있다.
[선형대수학] Linear Equation(일차방정식)
Linear Equation(일차방정식) n개의 변수 x1+x2+…anxn의 linear equation은 다음과 같은 형태를 가진다. a1x1+a2x2+…anxn=b 여기서 a1, a2, … an 부분을 coefficient라고 한다.
gbdai.tistory.com
Row reduction algorithm으로 구한 Row echelon form(기약 행사다리꼴)을 통해 linear system의 solution을 알 수 있다.
다음과 같은 augmented matrix(첨가행렬)이 있다고 해보자
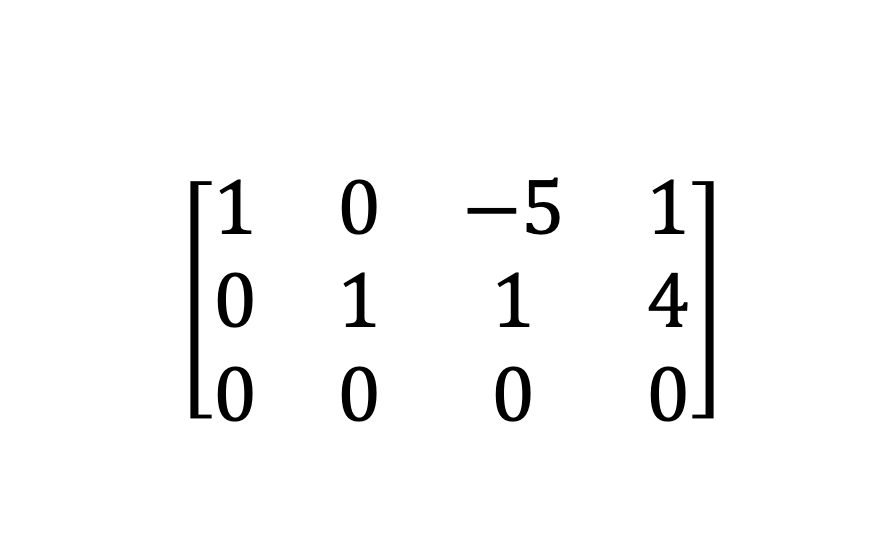
해당 augmented matrix(첨가행렬)를 linear equation으로 표현해보면 다음과 같다.

그런데, 위 연립방정식은 x3를 어떻게 선택하느냐에 따라 해가 여러개 존재한다.
예를 들어, x1=6,x2=3x3=1의 해가 있을 수 있고, $x_1 = -9, x_2 = 6 x_3 = -2$의 해가 존재하기도 한다.
이렇게, 무수히 많은 해를 일일히 표현할 수 없기 때문에 다음과 같이 표현한다.
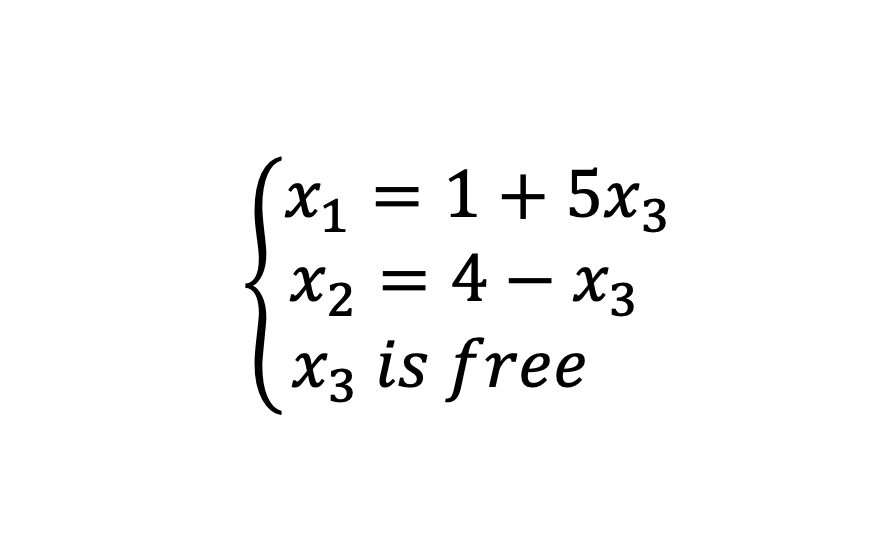
x3을 free variable으로 두고, 나머지 variable들을 free variable로 표현한다.
이 때, leading position에 있는 변수들을 basic variable(free variable로 표현되는 변수)로 두고, 그 외의 변수들은 free variable로 둔다.
basic variable은 leading position에 있기 때문에 leading variable이라고도 한다.
또한, 위와 같이 basic variable과 free variable로 표현된 linear system의 solution을 general solution(일반해)라고 한다.
이제까지 Row reduction algorithm과 general solution에 대해 알아보았다. 이 두 가지와 linear system의 solution은 매우 밀접한 관계를 지니는데, 이와 관련된 이론을 Existence and Uniqueness Theorem이라고 하며, 다음과 같다.
- Linear system이 consitent(해가 존재함)하면, row reduction을 통해 얻은 echelon form(행사다리꼴)에 [0 … 0 b]와 같은 행이 없어야 해가 존재한다.
- Linear system이 consitent(해가 존재함)하면, free variable이 없으면 unique solution을 가지고(해가 하나), free variable이 있으면 infinity solution(무한히 많은 해)을 가진다.
'MATH' 카테고리의 다른 글
| [선형대수학] Orthogonality(직교성) (0) | 2022.12.17 |
|---|---|
| [선형대수학] Inner product(내적)와 Length, Distance (0) | 2022.12.17 |
| [선형대수학] Linear Equation(일차방정식) (0) | 2022.09.17 |


댓글