Inner product(내적)

다음과 같은 u와 v, 두 개의 벡터가 주어졌을 때 inner product는 가운데 위치한 수식처럼 u의 transpose에 v를 곱해주는 것으로 정의된다.
예시를 통해 알아보자

다음과 같은 u와 v를 inner product를 취해주면 다음과 같은 과정을 통해 -1이라는 값이 나오는 것을 확인할 수 있다.
이때, 순서를 바꾸어서 inner product를 취해도 같은 결과가 나오게 된다.
그렇다면, 이러한 inner product는 어떠한 특징을 가지고 있을까? 특징은 다음과 같다.

- 앞서 살펴본것처럼 순서를 바꾸어서 inner product를 취해도 값은 같다.
- 분배 법칙이 적용된다.
- 스칼라곱을 취한 vector와 다른 vector를 Inner product를 취할 때 inner product 먼저 계산하고 그 이후에 스칼라곱을 적용해도 결과가 같다.
- 영 벡터가 아닌 이상 같은 벡터에 대한 Inner product는 항상 0보다 크다. 영 벡터 일 경우에는 0이 된다.
Length
금방까지 살펴본 inner product를 통해 vector의 길이인 length를 알 수 있다.
length는 norm이라고도 하며, 다음과 같이 해당 vector 스스로 inner product를 취해 그 값에 루트를 씌워주면 구할 수 있다.

스칼라곱이 적용된 vector의 경우, 해당 스칼라를 따로 빼서 절댓값을 취해주고, 남은 vector의 length와 곱해줘도 같은 결과를 얻을 수 있다.
Unit vector라는 개념도 여기서 등장하게 되는데, vector의 length가 1인 vector를 unit vector라고 하며,
같은 방향에 있는 vector를 length로 나눠주어 length가 1이 되게끔 하는 작업을 normalizing이라고 한다.
이러한 length와 normalizing의 예시는 다음과 같다.

자체적으로 inner product를 취하는거니깐 각 element들을 제곱하여 더해주고, 그 값을 루트를 씌워주면 vector v의 length는 3이라는 것을 알 수 있다.
이때, length를 구했기 때문에 normalizing도 취할 수 있다.
length인 3으로 각 element를 나눠주면 아래와 같은 vector가 나오고, 당연하게도 해당 vector의 length는 1 임을 확인할 수 있다.
Distance
Length를 조금만 변형하면, 두 vector 간의 거리, distance를 구할 수 있다.
u와 v라는 vector가 주어졌을 때, 두 벡터간의 거리는 u−v 벡터의 길이를 구함을 통해 확인할 수 있다.
다음의 예시를 같이 살펴보자

위의 예시는 ||u−v||을 나타낸 예시이다. 그렇다면, 왜 두 벡터 간의 거리가 u−v 벡터의 길이가 될까?
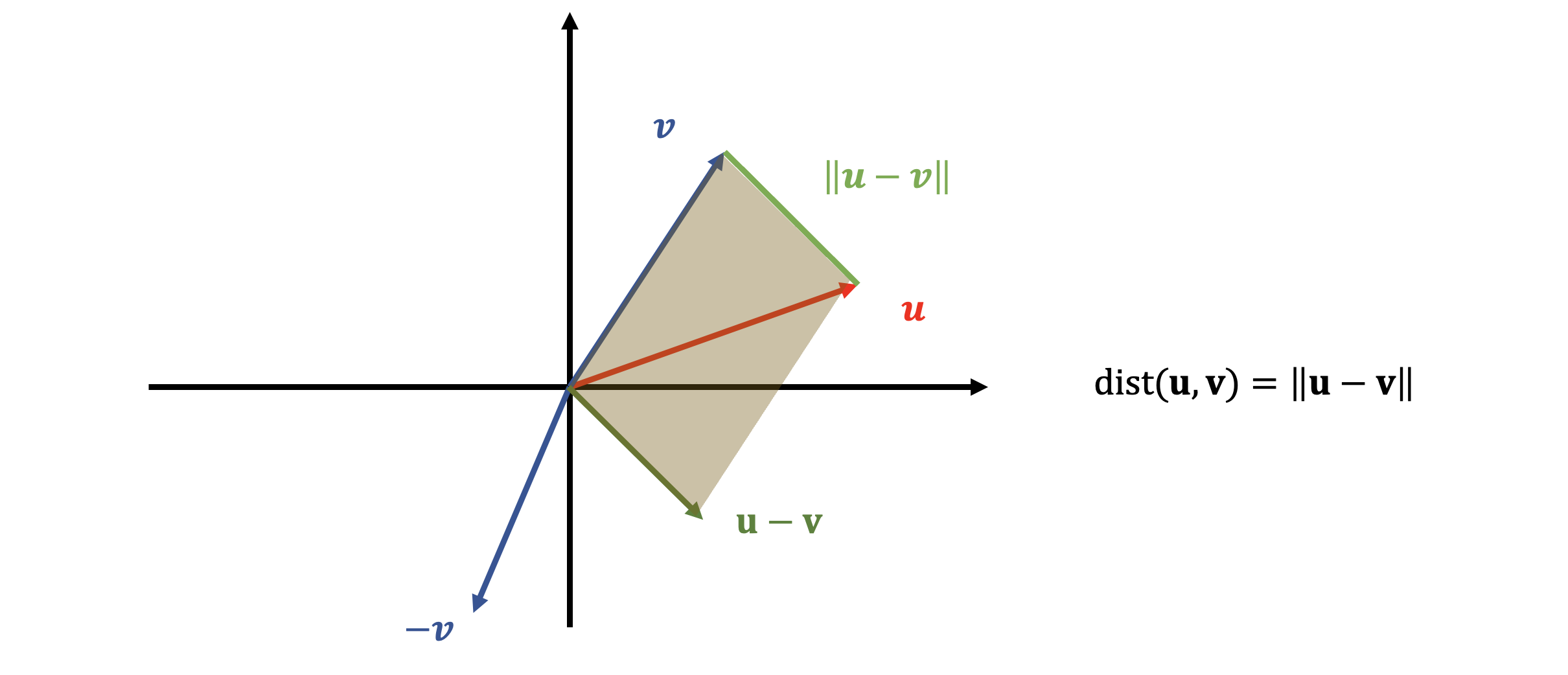
다음의 예시는 그 이유를 설명해준다.
4분면에 위치한 u−v벡터와 v벡터가 평행사변형을 만드는데,
이를 통해 u벡터와 v벡터의 거리는 u−v 벡터의 길이와 같음을 확인할 수 있다.
'MATH' 카테고리의 다른 글
| [선형대수학] Orthogonality(직교성) (0) | 2022.12.17 |
|---|---|
| [선형대수학] Gauss-Jordan elimination(가우스-요르단 소거법)과 Solution of linear system (1) | 2022.12.06 |
| [선형대수학] Linear Equation(일차방정식) (0) | 2022.09.17 |


댓글